题目内容
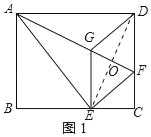
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF
GF![]() AF;
AF;
(3)若AB=4,BC=5,求GF的长.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,得出∠DGF=∠DFG.证出GD=DF.因此DG=GE=DF=EF,即可得出结论;
(2)连接DE,交AF于点O.由菱形的性质得出GF⊥DE,OG=OF=![]() GF.证明△DOF∽△ADF,得出
GF.证明△DOF∽△ADF,得出![]() ,即DF2=FOAF,即可得出结论;
,即DF2=FOAF,即可得出结论;
(3)作GH⊥CD于H,则CH=EG,由(1)得:AE=AD,在Rt△ABE中,由勾股定理得出BE=![]() =3,得出EC=2.设GF=x,菱形边长为y,则由(2)得:y2=
=3,得出EC=2.设GF=x,菱形边长为y,则由(2)得:y2=![]() x×AF①,在Rt△ADF中,AF2 =25+y2②,在Rt△ECF中,y2=4+(4y)2③,解得:y=
x×AF①,在Rt△ADF中,AF2 =25+y2②,在Rt△ECF中,y2=4+(4y)2③,解得:y=![]() ,代入②得:AF=
,代入②得:AF=![]() ,再代入①得:x=
,再代入①得:x=![]() 即可.
即可.
解:(1)∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF,
∴四边形EFDG为菱形.
(2)如图1所示:连接DE,交AF于点O.
∵由(1)四边形EFDG为菱形.
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.
GFAF.
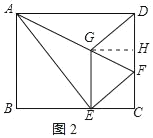
(3)作GH⊥CD于H,如图2所示:
则CH=EG,由(1)得:AE=AD,
在Rt△ABE中,AB=4,AE=AD=5,
∴BE=![]() =3,
=3,
∴EC=2.
设GF=x,菱形边长为y,则
由(2)得:y2=![]() x×AF①,
x×AF①,
在Rt△ADF中,AF2 =25+y2 ②
在Rt△ECF中,y2 =4+(4﹣y)2③
解得:y=![]() ,
,
代入②得:AF=![]() ,再代入①得:
,再代入①得:![]() .
.
即GF=![]() .
.