��Ŀ����
����Ŀ��Ϊӭ�ӡ���һ�������Ͷ��ڣ�ij�̳��ƻ������ס�������Ʒ�Ƶ�![]() ������100������֪��Ʒ��ÿ���Ľ��۱ȼ�Ʒ��ÿ���Ľ��۹�30Ԫ������120Ԫ�����Ʒ�Ƶļ���ǡ���ǹ�����Ʒ�Ƽ�����2����
������100������֪��Ʒ��ÿ���Ľ��۱ȼ�Ʒ��ÿ���Ľ��۹�30Ԫ������120Ԫ�����Ʒ�Ƶļ���ǡ���ǹ�����Ʒ�Ƽ�����2����
��1����ס�������Ʒ��ÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳�������Ʒ����ÿ��50Ԫ���ۣ���Ʒ����ÿ��100Ԫ���ۣ�Ϊ�����г�����������Ʒ�Ƶ���������������Ʒ��������4��������ȷ���������Ľ���������������������
���𰸡���1����Ʒ��ÿ���Ľ���Ϊ30Ԫ������Ʒ��ÿ���Ľ���Ϊ60Ԫ����2��������Ʒ��T����80����������Ʒ��T����20���������������2400Ԫ
��������
��1�����Ʒ��ÿ���Ľ���ΪxԪ������Ʒ��ÿ���Ľ���Ϊ��x+30��Ԫ�����á���120Ԫ�����Ʒ�Ƶļ���ǡ���ǹ�����Ʒ�Ƽ�����2�����з�����⼴�ɣ�
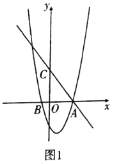
��2������̳�������Ʒ��T����y��������Ʒ��T������100-y�����������Ŀ�����õ�y�ķ�Χ�����г�����![]() ����y��һ�κ���������һ�κ��������ʽ��y��Χ�������.
����y��һ�κ���������һ�κ��������ʽ��y��Χ�������.
�⣺��1�����Ʒ��ÿ���Ľ���ΪxԪ������Ʒ��ÿ���Ľ���Ϊ��x+30��Ԫ��
�����⣬��![]()
�������߳�![]() ����
����
![]()
���![]()
���飬��![]() ʱ��
ʱ��![]()
���ԣ�ԭ��ʽ���̵Ľ�Ϊ![]()
�ʼ�Ʒ��ÿ���Ľ���Ϊ30Ԫ������Ʒ��ÿ���Ľ���Ϊ60Ԫ.
��2������̳�������Ʒ��T����y��������Ʒ��T������100-y��������
�߹�������Ʒ�Ƶ���������������Ʒ��������4��
��![]()
��![]()
�����⣬����![]()
![]()
��![]()
��W��y���������С
�൱![]() ʱ��W�����ֵΪ
ʱ��W�����ֵΪ![]() Ԫ
Ԫ
��������Ľ��������ǣ�������Ʒ��T����80����������Ʒ��T����20���������������2400Ԫ.

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�����Ŀ���������ǵ�����ˮƽ����ߣ����ýγ�Խ��Խ��ؽ����ͥ��С��������һ��С�γ�����������¼��7����ÿ����ʻ��·�̣����±�������50kmΪ��������50km�ļ�Ϊ��+��������50km�ļ�Ϊ���������պ�50km�ļ�Ϊ��0����
��һ�� | �ڶ��� | ������ | ������ | ������ | ������ | ������ | |
·�̣�km�� | ��9 | ��13 | 0 | ��14 | ��16 | +33 | +19 |
��1�������7�����ʻ·��������һ������ٵ�һ�����ʻ����ǧ�ף�
��2����ÿ��ʻ100km��������8����ÿ������6.5Ԫ������С������7������ͷ��ù��Ƕ���Ԫ��
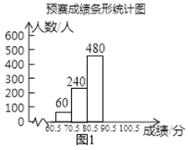
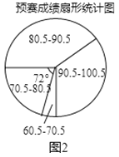
����Ŀ��Ϊ�˺����л����㴫ͳ�Ļ����úú��֣�ij��ѧ��չ��һ������ʫ����֪ʶ���������̹�����Ԥ���������;����������Σ�Ԥ���ɸ�����У�ȫԱ�μӣ���ͳһ�����֣�ͳ�Ƴɼ�����Ƴ���ͼ1��ͼ2��ʾ��������������Ԥ���ɼ�����ͳ��ͼ������Ԥ���ɼ�����ͳ��ͼ����Ԥ��ǰ10��ѡ�ֲμӸ������ɼ�����ǰ10��ѡ�ֳɼ�ͳ�Ʊ��������ðٷ��ƼǷ֣��÷ֶ�Ϊ60�����ϵ�������.
ǰ10��ѡ�ֳɼ�ͳ�Ʊ�
��� | �� | �� | �� | �� | �� | �� | �� | �� | �� | �� |
Ԥ���ɼ����֣� | 100 | 92 | 95 | 98 | 94 | 100 | 93 | 96 | 95 | 96 |
�����ɼ����֣� | 90 | 80 | 85 | 90 | 80 | 88 | 85 | 90 | 86 | 89 |
�ܳɼ����֣� | 94 | 84.8 | 89 |
| 85.6 | 92.8 | 88.2 |
| 89.6 | 91.8 |
��1�������ѧѧ����������������ͼ1����������
��2����ͼ2�У�����90.5��100.5��������������Բ�ĽǶ�����
��3��Ԥ��ǰ10��ѡ�ֲμӸ������ɼ�����ǰ10��ѡ�ֳɼ�ͳ�Ʊ���������Ԥ���ɼ�ռ40%�������ɼ�ռ60%�ı��������ܳɼ���������ѡ��3�˲μӾ���������Ϊѡ�ļ���ѡ��ȥ�μӾ�������˵������.