Question

如图，在边长为2的正三角形中，将其内切圆和三个角切圆（与角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为______．

Answer 1

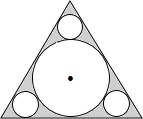
如图，连接OB、OD；
设小圆的圆心为P，⊙P与⊙O的切点为G；过G作两圆的公切线EF，交AB于E，交BC于F，
则∠BEF=∠BFE=90°-30°=60°，所以△BEF是等边三角形．
在Rt△OBD中，∠OBD=30°，
则OD=BD•tan30°=1×

3

3

=

3

3

，OB=2OD=

2 3

3

，BG=OB-OG=

3

3

；
由于⊙P是等边△BEF的内切圆，所以点P是△BEF的内心，也是重心，
故PG=

1

3

BG=

3

9

；
∴S_⊙O=π×（

3

3

）²=

1

3

π，S_⊙P=π×（

3

9

）²=

1

27

π；
∴S_阴影=S_△ABC-S_⊙O-3S_⊙P=

3

-

1

3

π-

1

9

π=

3

-

4

9

π．
故答案为

3

-

4

9

π．