题目内容
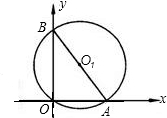
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=
,求BD和BC的长.
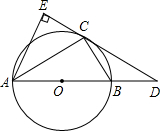
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=
| 24 |
| 5 |

(1)证明:连接OC;
∵AC平分∠EAB,
∴∠EAC=∠BAC;
又在圆中OA=OC,
∴∠AC0=∠BAC,
∴∠EAC=∠ACO,
∴OC∥AE(内错角相等,两直线平行);
则由AE⊥DC知OC⊥DC,
即DC是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°,
∴△DCO∽△DEA,
∴
=
,
∴
=
,
∴
=
,
∴BD=2;
∵Rt△EAC∽Rt△CAB,
∴
=
,
∴
=
∴AC2=
,
由勾股定理得:
BC=
.

∵AC平分∠EAB,
∴∠EAC=∠BAC;
又在圆中OA=OC,
∴∠AC0=∠BAC,
∴∠EAC=∠ACO,
∴OC∥AE(内错角相等,两直线平行);
则由AE⊥DC知OC⊥DC,
即DC是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°,
∴△DCO∽△DEA,
∴
| DO |
| AD |
| CO |
| AE |
∴
| DB+BO |
| AB+BD |
| CO |
| AE |
∴
| DB+3 |
| 6+BD |
| 3 | ||
|
∴BD=2;
∵Rt△EAC∽Rt△CAB,
∴
| EA |
| AC |
| AC |
| AB |
∴
| ||
| AC |
| AC |
| 6 |
∴AC2=
| 144 |
| 5 |
由勾股定理得:
BC=
6
| ||
| 5 |


练习册系列答案
相关题目