题目内容
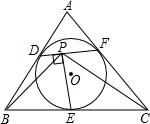
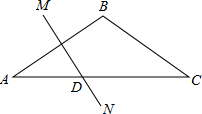
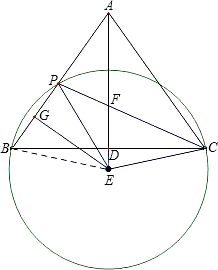
已知点D为等腰△ABC的底边BC的中点,P为AB线段内部的任意一点,设BP的垂直平分线与直线AD交于点E,PC与AD交于点F.求证:直线EP是△APF的外接圆的切线.
证明:∵EG垂直平分BP,
∴EP=BE,
∵AD是等腰三角形ABC底边上的高,
∴AD垂直平分BC,
∴BE=EC,
∴以E为圆心、EB为半径作圆E,则点P、C都在该圆的圆周上,
∴在Rt△ABD中,∠PAE=∠BAE=90°-∠ABC=90°-
∠PEC=∠EPC,
∵在等腰三角形EPC中,∠EPC=90°-
∠PEC,
∴∠PAE=∠EPC,
∴EP是△APF的外接圆的切线.
∴EP=BE,
∵AD是等腰三角形ABC底边上的高,
∴AD垂直平分BC,
∴BE=EC,
∴以E为圆心、EB为半径作圆E,则点P、C都在该圆的圆周上,
∴在Rt△ABD中,∠PAE=∠BAE=90°-∠ABC=90°-
| 1 |
| 2 |
∵在等腰三角形EPC中,∠EPC=90°-
| 1 |
| 2 |
∴∠PAE=∠EPC,
∴EP是△APF的外接圆的切线.


练习册系列答案
相关题目