��Ŀ����
����Ŀ��ӿȪ�����й����۽�֮�磬��֪ij�۽���ֲ���ү���۽۳ɱ�Ϊ2Ԫ/ǧ�ˣ������δ��90���۽۵����۵���p��Ԫ/ǧ�ˣ���ʱ��t���죩֮��ĺ�����ϵʽΪp=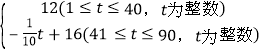 �����۽۵�������y��ǧ�ˣ���ʱ��t���죩����һ�κ�����ϵ���䲿���������±���ʾ��
�����۽۵�������y��ǧ�ˣ���ʱ��t���죩����һ�κ�����ϵ���䲿���������±���ʾ��
ʱ��t/�� | 1 | 10 | 20 | 40 | 70 | 90 |
��������y/ǧ�� | 105 | 150 | 200 | 300 | 450 | 550 |
��1����y��t֮��ĺ�������ʽ��
��2����δ��90��������У�Ԥ����һ�����������������������������Ϊ����Ԫ��
��3����ʵ�����۵ĺ�50���У����ү����ÿ����1ǧ���۽۾;���nԪ����n��5�������ض�ͯ��Ϊ��ѧ�����۹����з��ү���֣�ǡ�ôӵ�51�쿪ʼ����ǰһ����ȣ��۳���������������������ռ��٣������n��ȡֵ��Χ��
���𰸡���1��y=5t+100����2��ǰ60����������������Ϊ3200Ԫ����3��n��ȡֵ��ΧΪ1.9��n��5��
��������
��1�����ô���ϵ���������������ʽ����2�����x�����������ΪwԪ����1��t��40ʱ��������w=��12-2����5t+100��=50t+1000����t=40ʱw���ֵΪ3000Ԫ����41��t��90ʱ��w=��5t+100����-![]() t+16-2��=-
t+16-2��=-![]() t2+60t+1400����������ֵ����3����ÿ��۳������������������ΪmԪ��������m=��5t+100����-
t2+60t+1400����������ֵ����3����ÿ��۳������������������ΪmԪ��������m=��5t+100����-![]() t+16-2��-��5t+100��n=-
t+16-2��-��5t+100��n=-![]() t2+��60-5n��t+1400-100n������ʵ�ʵ�49.5��60-5n��50.5��1.9��n��2.1���ɽ�һ�����n��ȡֵ��Χ.
t2+��60-5n��t+1400-100n������ʵ�ʵ�49.5��60-5n��50.5��1.9��n��2.1���ɽ�һ�����n��ȡֵ��Χ.
�⣺��1����y=kt+b����t=1��y=105��t=10��y=150����õ���![]() ��
��
��ã�![]() ��
��
��y=5t+100��
��2�����x�����������ΪwԪ��
��1��t��40ʱ��������w=��12-2����5t+100��=50t+1000��
��t=40ʱw���ֵΪ3000Ԫ��
��41��t��90ʱ��w=��5t+100����-![]() t+16-2��=-
t+16-2��=-![]() t2+60t+1400��
t2+60t+1400��
�߶Գ���t=60��a=-![]() ��0��
��0��
���ڶԳ������w��x���������
��t=60ʱ��w���ֵ=3200��
��������ǰ60����������������Ϊ3200Ԫ��
��3����ÿ��۳������������������ΪmԪ��
������m=��5t+100����-![]() t+16-2��-��5t+100��n=-
t+16-2��-��5t+100��n=-![]() t2+��60-5n��t+1400-100n��
t2+��60-5n��t+1400-100n��
���ں�50���У�ÿ��۳��������������������ʱ��t����������٣�
��49.5��60-5n��50.5��
��1.9��n��2.1��
�֡�n��5��
��n��ȡֵ��ΧΪ1.9��n��5��

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�