题目内容
【题目】如图,已知等腰三角形![]() 是线段
是线段![]() 上的一点,连结
上的一点,连结![]() ,且有
,且有![]() .
.
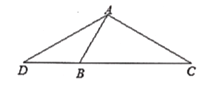
(1)若![]() ,求
,求![]() 的长;
的长;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)3;(2)见解析.
【解析】
(1)设∠C=x,根据等腰三角形的性质可得∠C=∠D,∠D=∠DAB,结合三角形外角的性质可得∠ABC=∠C,根据∠BAC=90°,可求得∠C=30°,解直角三角形可得AB=1,BC=2,即可求CD的长;
(2)由于![]() ,设AB=BD=a,所以CD=3a,证明△DAB∽△DCA,则可得
,设AB=BD=a,所以CD=3a,证明△DAB∽△DCA,则可得![]() =
=![]() ,求出AD=AC=
,求出AD=AC=![]() a,可得
a,可得![]() ,由勾股定理的逆定理得△ABC是直角三角形,∠BAC=90°.
,由勾股定理的逆定理得△ABC是直角三角形,∠BAC=90°.
解:(1)设![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)设![]() ,∵
,∵![]()
∴![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为直角三角形,
为直角三角形,![]() .
.
故答案为:(1)3;(2)见解析.

练习册系列答案
相关题目
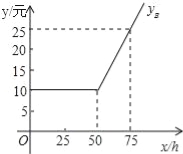
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?