题目内容
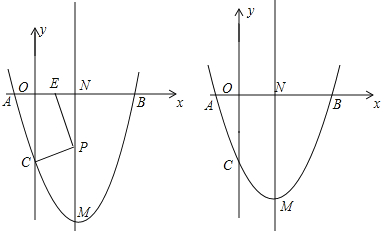
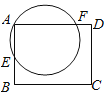
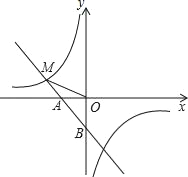
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
【答案】(1)y=﹣![]() ;(2)﹣2<x<0或x>1;(3)
;(2)﹣2<x<0或x>1;(3)![]()
【解析】
(1)先把M(-2,m)代入y=-x-1求出m得到M(-2,1),然后把M点坐标代入y=![]() 中可求出k的值,从而得到反比例函数解析式;
中可求出k的值,从而得到反比例函数解析式;
(2)通过解方程组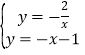 得反比例函数与一次函数的另一个交点坐标为(1,-2),然后写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
得反比例函数与一次函数的另一个交点坐标为(1,-2),然后写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可;
(3)设点B到直线OM的距离为h,然后利用面积法得到![]()
![]() h=1,于是解方程即可,
h=1,于是解方程即可,
解:(1)把M(﹣2,m)代入y=﹣x﹣1得m=2﹣1=1,则M(﹣2,1),
把M(﹣2,1)代入y=![]() 得k=﹣2×1=﹣2,
得k=﹣2×1=﹣2,
所以反比例函数解析式为y=﹣![]() ;
;
(2)解方程组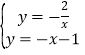 得
得![]() 或
或![]() ,
,
则反比例函数与一次函数的另一个交点坐标为(1,﹣2),
当﹣2<x<0或x>1时,y2>y1;
(3)OM=![]() =
=![]() ,S△OMB=
,S△OMB=![]() ×1×2=1,
×1×2=1,
设点B到直线OM的距离为h,
![]()
![]() h=1,解得h=
h=1,解得h=![]() ,
,
即点B到直线OM的距离为![]() .
.

【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
5分以下 | 3 | 0.06 | |
合计 | 50 | 1 |
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
![]()