题目内容
【题目】
地和
地之间的铁路交通设有特快列车和普通列车两种车次，某天一辆普通列车从A地出发匀速驶向地，同时另一辆特快列车从地出发匀速驶向地，两车与地的距离
（千米）与行驶时间
（时）的函数关系如图所示.
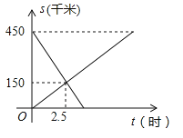
（1）地到地的距离为 千米，普通列车到达地所用时间为 小时；
（2）求特快列车与地的距离与的函数关系式；
（3）在、两地之间有一座铁路桥，特快列车到铁路桥后又行驶
小时与普通列车相遇，直接写出地与铁路桥之间的距离 .
【答案】（1）
千米，7.5小时；（2）
；（3）
千米
【解析】
（1）根据函数图象可以解答本题；
（2）根据函数图象中的数据可以求得特快列车与
地的距离s与t之间的函数关系式；
（3）根据图象可知两车相遇时间为2.5小时，从而可以得到特快列车到桥用的时间为2小时，然后根据（2）中的函数解析式即可解答本题．
（1） 由图象可得，地到
地的距离为千米，
普通列车到达地所用时间为：
（小时），
（2）设特快列车与地的距离
与
之间的函数关系式是
，
已知点（0， 450），（2.5,150）在直线，
∴把点（0， 450）与（2.5,150）代入函数解析式得
，解得
，
即特快列车与地的距离与之间的函数关系式是；
（3）设地与铁路桥之间的距离是
千米，
，
答：地与铁路桥之间的距离是千米.
阳光课堂课时作业系列答案
【题目】已知绿茶每千克成本50元，经研究发现销量y（kg）随销售单价x（元/kg）的变化而变化，具体变化规律如表所示：
销售单价x（元/kg） | … | 70 | 75 | 80 | 85 | 90 | … |
月销售量y（kg） | … | 100 | 90 | 80 | 70 | 60 | … |
（1）请根据上表，写出y与x之间的函数关系式（不必写出自变量x的取值范围）；
（2）若该绿茶的月销售利润为w（元），且售单价得高于80元，求w与x之间的函数关系式，并求出x为何值时，w的值最大？
（3）已知商家经销一种绿茶，用于装修门面已投资3000元，在第一个月，按使w获得最大值的销售单价进行销售后；在第二个月受物价部门干预，销售单价不得高于78元，要想在全部收回装修投资的基础上使这两个月的总利润至少达到1722元，求第二个月的销售单价的取值范围？
