题目内容
【题目】某校数学课外小组，在坐标纸上为某湿地公园的一块空地设计植树方案如下：第k棵树种植在点Pk（xk，yk）处，其中x1＝1，y1＝1，且k≥2时，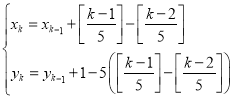
，[a]表示非负实数a的整数部分，例如[2.3]＝2，
，[0.5]＝0．按此方案，第2019棵树种植点的坐标应为（ ）
A.(6，2020)B.(2019，5)C.(3，403)D.(404，4)
【答案】D
【解析】
根据已知分别求出1≤k≤5时，P点坐标为（1，1）、（1，2）、（1，3）、（1，4）、（1，5），当6≤k≤10时，P点坐标为（2，1）、（2，2）、（2，3）、（2，4）、（2，5），通过观察得到点的坐标特点，进而求解．
解：由题可知1≤k≤5时，P点坐标为（1，1）、（1，2）、（1，3）、（1，4）、（1，5），
当6≤k≤10时，P点坐标为（2，1）、（2，2）、（2，3）、（2，4）、（2，5），
……
通过以上数据可得，P点的纵坐标5个一组循环，
∵2019÷5＝403…4，
∴当k＝2019时，P点的纵坐标是4，横坐标是403+1＝404，
∴P（404，4），
故选：D．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
