Question

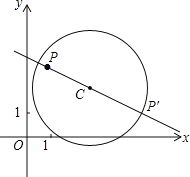
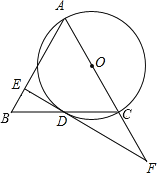
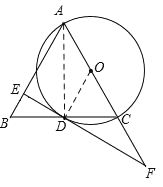
【题目】如图，以等腰△ABC的一腰AC为直径作⊙O，交底边BC于点D，过点D作腰AB的垂线，垂足为E，交AC的延长线于点F．

（1）求证：EF是⊙O的切线；

（2）证明：∠CAD＝∠CDF；

（3）若∠F＝30°，AD＝，求⊙O的面积．

Answer 1

【答案】（1）见解析；（2）见解析；（3）π

【解析】

（1）连接OD，AD，证点D是BC的中点，由三角形中位线定理证OD∥AB，可推出∠ODF＝90°，即可得到结论；

（2）由OD＝OC得到∠ODC＝∠OCD，由∠CAD+∠OCD＝90°和∠CDF+∠ODC＝90°即可推出∠CAD＝∠CDF；

（3）由∠F＝30°得到∠DOC＝60°，推出∠DAC＝30°，在Rt△ADC中，由锐角三角函数可求出AC的长，推出⊙O的半径，即可求出⊙O的面积．

解:（1）证明：如图，连接OD，AD，

∵AC是直径，

∴∠ADC＝90°，即AD⊥BC，

又AB＝AC，

∴BD＝CD，

又AO＝CO，

∴OD∥AB，

又FE⊥AB，

∴FE⊥OD，

∴EF是⊙O的切线；

（2）∵OD＝OC，

∴∠ODC＝∠OCD，

∵∠ADC＝∠ODF＝90°，

∴∠CAD+∠OCD＝90°，∠CDF+∠ODC＝90°，

∴∠CAD＝∠CDF；

（3）在Rt△ODF中，∠F＝30°，

∴∠DOC＝90°﹣30°＝60°，

∵OA＝OD，

∴∠OAD＝∠ODA＝∠DOC＝30°，

在Rt△ADC中，

AC＝ ＝＝2，

∴r＝1，

∴S⊙O＝π12＝π，

∴⊙O的面积为π．