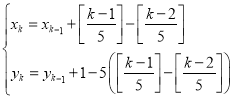题目内容
【题目】下面是小东设计的“作圆的一个内接矩形,并使其对角线的夹角为60°”的尺规作图过程
已知:⊙O
求作:矩形ABCD,使得矩形ABCD内接于⊙O,且其对角线AC,BD的夹角为60°.
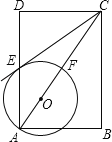
作法:如图
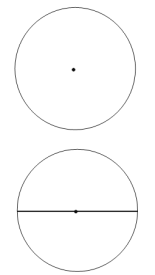
①作⊙O的直径AC;
②以点A为圆心,AO长为半径画弧,交直线AC上方的圆弧于点B;
③连接BO并延长交⊙O于点D;
所以四边形ABCD就是所求作的矩形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点A,C都在⊙O上,
∴OA=OC
同理OB=OD
∴四边形ABCD是平行四边形
∵AC是⊙O的直径,
∴∠ABC=90° ( )(填推理的依据)
∴四边形ABCD是矩形
∵AB= =BO,
∴四边形ABCD四所求作的矩形
【答案】(1)答案见解析(2)答案见解析.
【解析】
(1)根据要求作图即可得;
(2)根据圆周角定理推论及圆的性质求解可得.
(1)如图所示,矩形ABCD即为所求;
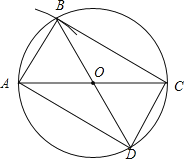
(2)证明:∵点A,C都在⊙O上,
∴OA=OC
同理OB=OD
∴四边形ABCD是平行四边形
∵AC是⊙O的直径,
∴∠ABC=90°(直径所对圆周角是直角)
∴四边形ABCD是矩形
∵AB=AO=BO,
∴四边形ABCD即为所求作的矩形,
故答案为直径所对圆周角是直角,AO.

练习册系列答案
相关题目