题目内容
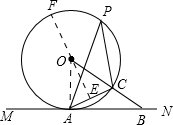
如图，已知直线MN经过⊙O上的点A，点B在MN上，连OB交⊙O于C点，且点C是OB的中点，AC=
OB，若点P是⊙O上的一个动点，当AB=2
时，求△APC的面积的最大值．
| 1 |
| 2 |
| 3 |
连接OA；
∵C是OB的中点，且AC=
OB，
∴∠OAB=90°（2分），
∴∠O=60°，
∴OA=AC=2；
过点O作OE⊥AC于E，延长EO交圆于点F，则P（F）E是△PAC的AC边上的最大的高；（1分）
在△OAE中，OA=2，∠AOE=30°，
∴OE=
（1分），
∴PE=2+
（1分），
∴S△PAC=
AC•PE=
×2×(2+
)，
即S△PAC=2+
．（1分）
∵C是OB的中点，且AC=
| 1 |
| 2 |
∴∠OAB=90°（2分），
∴∠O=60°，
∴OA=AC=2；
过点O作OE⊥AC于E，延长EO交圆于点F，则P（F）E是△PAC的AC边上的最大的高；（1分）
在△OAE中，OA=2，∠AOE=30°，
∴OE=
| 3 |
∴PE=2+
| 3 |
∴S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
即S△PAC=2+
| 3 |
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
有一点D使∠ABD=30°，BD的中点为E，连接OE并延长OE与BC交于点C，连接CD．
