Question

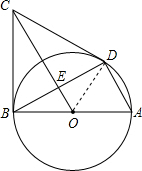
如图，已知AB是⊙O的直径，且AB为6，过B点作⊙O的切线CB与⊙O相切于点B，在半圆AB上有一点D使∠ABD=30°，BD的中点为E，连接OE并延长OE与BC交于点C，连接CD．
（1）求证：CD是⊙O的切线．
（2）四边形ABCD的周长是多少？

Answer 1

（1）证明：连接OD，
∵OE是BD的中点且BO=DO，
∴OE⊥BD，
∴CE⊥BD，
∵BE=DE，
∴BC=DC，
∵OB=OD，OC=OC，
∴△OBC≌△ODC，
∵BC是⊙O的切线，
∴∠OBC=90°，
∴∠ODC=90°，
∴CD是⊙O的切线；

（2）∵BC是⊙O的切线，
∴∠OBC=90°，
∵∠ABD=30°，
∴∠DBC=60°，
∵BC=CD，
∴∠DBC=∠BDC=60°，
∴△BCD是等边三角形，
∴BC=BD=CD，
∵AB是直径，
∴∠ADB=90°，
∵∠ABD=30°，AB=6，
∴AD=

1

2

AB=

1

2

×=3，BD=

AB2-AD2

=

62-32

=3

3

，
∴四边形ABCD的周长为：3

3

+3

3

+3+6=9+6

3

．