题目内容
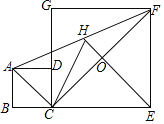
【题目】如图,正方形ABCD和正方形CEFC中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.
(1)求证:HC=HF.
(2)求HE的长.
【答案】(1)见解析;(2)HE=![]() .
.
【解析】
(1)利用直角三角形斜边上的中线等于斜边的一半求解即可;
(2)分别求得HO和OE的长后即可求得HE的长.
(1)证明:∵AC、CF分别是正方形ABCD和正方形CGFE的对角线,
∴∠ACD=∠GCF=45°,
∴∠ACF=90°,
又∵H是AF的中点,
∴CH=HF;
(2)∵CH=HF,EC=EF,
∴点H和点E都在线段CF的中垂线上,
∴HE是CF的中垂线,
∴点H和点O是线段AF和CF的中点,
∴OH=![]() AC,
AC,
在Rt△ACD和Rt△CEF中,AD=DC=1,CE=EF=3,
∴AC=![]() ,
,
∴CF=3![]() ,
,
又OE是等腰直角△CEF斜边上的高,
∴OE=![]() ,
,
∴HE=HO+OE=2![]() ;
;

练习册系列答案
相关题目