Question

【题目】已知直线l为x+y=8，点P（x，y）在l上且x＞0，y＞0，点A的坐标为（6，0）．

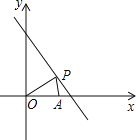
（1）设△OPA的面积为S，求S与x的函数关系式，并直接写出x的取值范围；

（2）当S=9时，求点P的坐标；

（3）在直线l上有一点M，使OM+MA的和最小，求点M的坐标．

Answer 1

【答案】（1）、y=24﹣3x（0＜x＜8）；（2）、P（5,3）；（3）、（6.4，1.6）.

【解析】

试题分析：（1）、根据点P在直线x+y=8上得出点P的纵坐标，然后根据三角形的面积计算法则求出函数解析式；（2）、将y=9代入函数解析式，从而得出点P的坐标；（3）、首先得出点O关于l的对称点B的坐标为（8，8），然后求出直线AB的函数解析式，然后根据两直线的交点求法得出交点的坐标.

试题解析：（1）、∵点P（x，y）在直线x+y=8上， ∴y=8﹣x， ∵点A的坐标为（6，0），

∴S=6××（8﹣x）=24﹣3x，（0＜x＜8）；

（2）、当24﹣3x=9时，x=5，即P的坐标为（5，3）．

（3）、点O关于l的对称点B的坐标为（8，8），设直线AB的解析式为y=kx+b，

根据题意可得：

解得：，

故直线AB的解析式为y=4x﹣24，

由

解得：

点M的坐标为（6.4，1.6）．