��Ŀ����
����Ŀ������ͼ��������Խ��ʹ������ʽ����ȷ�ԣ�Ҳ���Խ��Ͳ���ʽ����ȷ�ԣ�
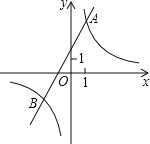
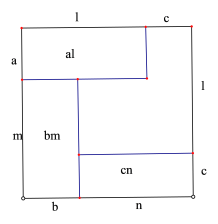
��1������������ʾͼ��д��һ���������ʽ ��
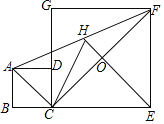
��2����֪����a��b��c��m��n��l������ambnclk���Թ���߳�Ϊk�������Σ�����ͼ�������˵��albmcnk2��
˼���������£�
��Ϊambnclk������a��b��c��m��n��l���� k����������������С������������k2���Կ���һ�������ε��������al��bm��cn���Էֱ����������ε�������뻭��ͼ�Σ�������ͼ�������˵��albmcnk2��

���𰸡���1��![]() ����2��С�ڣ����ɼ���⣮
����2��С�ڣ����ɼ���⣮
��������
��1���ȷֱ��ʾ���������ε����Ϊ![]() ��С���������Ϊ
��С���������Ϊ![]() ����Ӱ�������Ϊ
����Ӱ�������Ϊ![]() ���ٸ���С�����ε����+4�������ε����=����������������ɵõ��𰸣�
���ٸ���С�����ε����+4�������ε����=����������������ɵõ��𰸣�
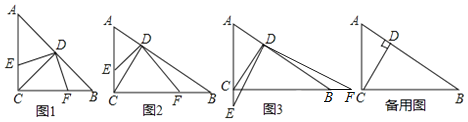
��2����������ָ�����������Σ�ʹ��߳�����ambnclk����a��b��c��m��n��l�����������������б߳�Ϊa��l��b��m��c��n�ij����Σ�����ͨ�������Σ����ɵõ�albmcnk2��
��1����С�����ε����+4�������ε����=�������������
��![]() ��
��
�ʴ��ǣ�![]() ��
��
��2������һ���߳�Ϊk�������Σ���ͼ��ʾ����Ȼ���㣺ambnclk��
����ͼ�ο�֪���������ڲ�3�������ε����֮��С�������ε����������albmcnk2��

 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�