Question

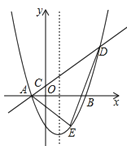
【题目】如图，在平面直角坐标系中，抛物线y＝ax2－2ax－3a（a＞0）与x轴交于A，B两点（点A在点B左侧），经过点A的直线l：y＝kx＋b与y轴交于点C，与抛物线的另一个交点为D，且CD＝4AC．

（1）求点A的坐标及直线l的函数表达式（其中k，b用含a的式子表示）；

（2）点E为直线l下方抛物线上一点，当△ADE的面积的最大值为时，求抛物线的函数表达式．

Answer 1

【答案】（1）A（－1，0），y＝ax＋a；（2）y＝x2－x－．

【解析】分析：（1）由抛物线y=ax2﹣2ax﹣3a（a＜0）与x轴交于两点A、B，求得A点的坐标，作DF⊥x轴于F，根据平行线分线段成比例定理求得D的坐标，然后利用待定系数法法即可求得直线l的函数表达式．

（2）设点E（m，ax2﹣2ax﹣3a），知HE=（ax+a）﹣（ax2﹣2ax﹣3a）=﹣ax2+3ax+4a，根据直线和抛物线解析式求得点D的横坐标，由S△ADE=S△AEH+S△DEH列出函数解析式，根据最值确定a的值即可．

详解：（1）令y=0，则ax2﹣2ax﹣3a=0，解得：x1=﹣1，x2=3．

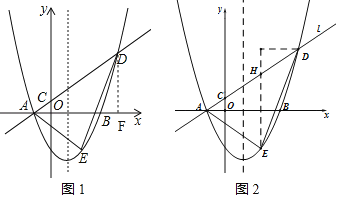
∵点A在点B的左侧，∴A（﹣1，0），如图1，作DF⊥x轴于F，

∴DF∥OC，∴=．

∵CD=4AC，∴==4．

∵OA=1，∴OF=4，∴D点的横坐标为4，代入y=ax2﹣2ax﹣3a得：y=5a，∴D（4，5a），把A、D坐标代入y=kx+b得，解得： ，∴直线l的函数表达式为y=ax+a．

（2）如图2，过点E作EH∥y轴，交直线l于点H，

设E（x，ax2﹣2ax﹣3a），则H（x，ax+a），∴HE=（ax+a）﹣（ax2﹣2ax﹣3a）=﹣ax2+3ax+4a，由，得x=﹣1或x=4，即点D的横坐标为4，∴S△ADE=S△AEH+S△DEH=（﹣ax2+3ax+4a）=﹣a（x﹣）2+a，∴△ADE的面积的最大值为a，∴a=，解得：a=，∴抛物线的函数表达式为y=x2﹣x﹣．