题目内容

反比例函数y=
6
x
与y=
3
x
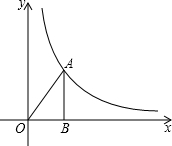
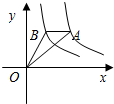
在第一象限的图象如图所示，作一条平行于x轴的直线分别交双曲线于A、B两点，连接OA、OB，则△AOB的面积为（　　）
A．
3
2
B．2C．3D．1

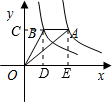
分别过A、B作x轴的垂线，垂足分别为D、E，过B作BC⊥y轴，点C为垂足，
∵由反比例函数系数k的几何意义可知，S四边形OEAC=6，S△AOE=3，S△BOC=
3
2
，
∴S△AOB=S四边形OEAC-S△AOE-S△BOC=6-3-
3
2
=
3
2
．
故选A．
练习册系列答案
相关题目
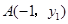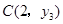已知点，，在反比例函数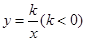的图象上，则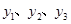的大小关系为_________（用“>”或“<”连接）.
如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，-3），反比例函数y=
k
x
的图象经过点C，一次函数y=ax+b的图象经过点A、C，
（1）求反比例函数与一次函数的解析式；
（2）求点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．
如图、点A为双曲线上一点，AB⊥x轴，SOAB=3，则双曲线的解析式为（　　）
A．y=
3
x
B．y=
x
3
C．y=
6
x
D．y=-
6
x
如图，直线y=kx（k＞0）与双曲线y=
2
x
交于A，B两点，若A，B两点的坐标分别为A（x1，y1），B（x2，y2），则x1y2+x2y1的值为（　　）
A．-8B．4C．-4D．0
如图，反比例函数y1=
k1
x
和正比例函数y2=k2x的图象都经过点A（-1，2），若y1＞y2，则x的取值范围是（　　）
A．-1＜x＜0B．-1＜x＜1
C．x＜-1或0＜x＜1D．-1＜x＜0或x＞1
如图，直线y=x+2与双曲线y=
m-3
x
在第二象限有两个交点，那么m的取值范围在数轴上表示为（　　）
A．B．
C．D．
如图，直线y=
3
x-2与双曲线y=
k
x
（k＞0）在第一象限内的交点为R，与x轴的交点为P，与y轴的交点为Q；作RM⊥x轴于点M，若△OPQ与△PRM的面积是4：1，则k等于（　　）
A．
2
3
3
B．
3
C．2D．3
已知反比例函数y=-
a2+1
x
的图象上有点A（x1，y1），B（x2，y2），C（x3，y3），且x1＞x2＞0＞x3，则关于y1，y2，y3大小关系正确的是（　　）
A．y1＞y2＞y3B．y2＞y1＞y3C．y1＞y3＞y2D．y3＞y1＞y2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网