Question

【题目】一个学生荡秋千，秋千链子的长度为，当秋千向两边摆动时，摆角（指摆到最高位置时的秋千与铅垂线的夹角）恰好是，则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.（结果可以保留根号）

Answer 1

【答案】

【解析】

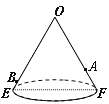
设秋千摆至最低点时的位置为C，连结AB，交OC于D．当秋千摆至最低点C时，点C为弧AB的中点，由垂径定理的推论知AB⊥OC，AD=BD，再解直角△AOD，求得OD，进而求出DC即可．

如图，设秋千摆至最低点时的位置为C，连结AB，交OC于D．

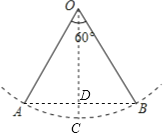
∵点C为弧AB的中点，O为圆心，

∴AB⊥OC，AD=BD，弧AC=弧BC，

∵∠AOB=60°，

∴∠AOC=30°．

∵OA=OB=OC=3，

∴AD=OA=，OD=，

∴DC=OC-OD=，

即它摆动至最高位置与最低位置的高度之差为（）m．

故答案为（）m．