题目内容
【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
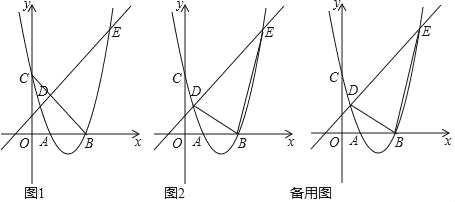
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
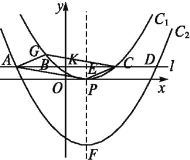
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,![]() 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值.
【答案】(1)y=![]() (x-3)2(2)①当m=
(x-3)2(2)①当m=![]() 时,四边形APCG是平行四边形②
时,四边形APCG是平行四边形②![]()
【解析】
(1)直接利用待定系数法求二次函数解析式得出即可;
(2)首先得出△GQK≌△POK(ASA),进而得出顶点G在抛物线C1上,得出2m2=![]() (-3-3)2,进而得出答案;
(-3-3)2,进而得出答案;
(3)利用函数对称性表示出A点坐标,再表示出KC,PF的长,进而得出其比值.
(1)∵抛物线C1过点(0,1),∴1=a(0-3)2,解得a=![]()
∴抛物线C1的解析式为y=![]() (x-3)2.
(x-3)2.
(2)①连接PG,∵点A,C关于y轴对称,
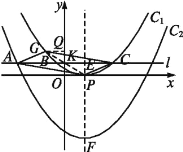
∴点K为AC的中点.
若四边形APCG是平行四边形,则必有点K是PG的中点.
过点G作GQ⊥y轴于点Q,
可得△GQK≌△POK,
∴GQ=PO=3,KQ=OK=m2,OQ=2m2.
∴点G(-3,2m2).
∵顶点G在抛物线C1上,∴2m2=![]() (-3-3)2,
(-3-3)2,
解得m=±![]() ,又m>0,∴m=
,又m>0,∴m=![]()
∴当m=![]() 时,四边形APCG是平行四边形.
时,四边形APCG是平行四边形.
②不会.在抛物线y=![]() (x-3)2中,令y=m2,
(x-3)2中,令y=m2,
解得x=3±3m,又m>0,且点C在点B的右侧,
∴C(3+3m,m2),KC=3+3m.
∵点A,C关于y轴对称,
∴A(-3-3m,m2).
∵抛物线C1向下平移h(h>0)个单位得到抛物线C2,∴抛物线C2的解析式为y=![]() (x-3)2-h.
(x-3)2-h.
∴m2=![]() (-3-3m-3)2-h,
(-3-3m-3)2-h,
解得h=4m+4,
∴PF=4+4m.
![]() .
.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案