题目内容
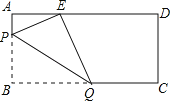
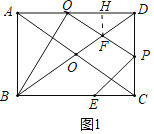
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,AB=3cm,BC=4cm,点E是BC上一点,且CE=1cm.点P由点C出发,沿CD方向向点D匀速运动,速度为1cm/s;点Q由点A出发,沿AD方向向点D匀速运动,速度为![]() cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
cm/s,点P,Q同时出发,PQ交BD于F,连接PE,QB,设运动时间为t(s)(0<t<3).
(1)当t为何值时,PE∥BD?
(2)设△FQD的面积为y(cm2),求y与t之间的函数关系式.
(3)是否存在某一时刻t,使得四边形BQPE的周长最小.若存在,求出此四边形BQPE的面积;若不存在,请说明理由.

【答案】(1)t=![]() ;(2)
;(2)![]() ;(3)存在,四边形BQPE的周长的最小值为3+
;(3)存在,四边形BQPE的周长的最小值为3+![]() .
.
【解析】
(1)当![]() 时,PE∥BD,由此构建方程即可解决问题.
时,PE∥BD,由此构建方程即可解决问题.
(2)作FH⊥DQ.首先证明QF∥OA,△QDF是等腰三角形,求出FH即可解决问题.
(3)如图2中,作B关于直线AD的对称点B′,点E关于直线CD的对称点E′,连接B′E′交AD于Q,交CD于P,连接BQ,PE.此时BQ+QP+PE+BE的值最小.
解:(1)∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=4,∠BAD=90°,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]()
![]() ,
,
∴t=![]() s时,PE∥BC.
s时,PE∥BC.
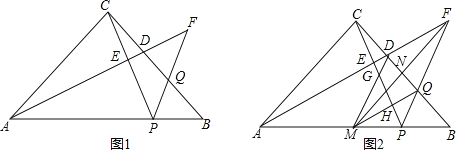
(2)如图1中,作FH⊥DQ.
![]() ,
,![]() ,
,
![]()
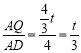 ,
,![]() ,
,
![]()
![]() ,
,
∴FQ∥OA,
∴∠FQD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠FDQ=∠FQD,
∴FQ=FD,∵FH⊥DQ,
![]() ,
,
![]() ,
,
![]()
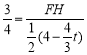 ,
,
![]() ,
,
∴![]() .
.
(3)如图2中,作B关于直线AD的对称点B′,点E关于直线CD的对称点E′,连接B′E′交AD于Q,交CD于P,连接BQ,PE.
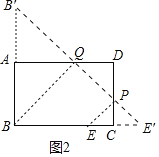
∵BQ+QP+PE+BE=B′Q+QP+PE′+BE=B′E′+BE=B′E′+3,
∴此时BQ+QP+PE+BE的值最小,
![]() ,
,
∴四边形BQPE的周长的最小值为3+![]() .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案