题目内容
【题目】在△ABC中,∠ACB=90°,AC=BC,点P在边AB上,点D、Q分别为边BC上的点,线段AD的延长线与线段PQ的延长线交于点F,连接CP交AF于点E,若∠BPF=∠APC,FD=FQ.
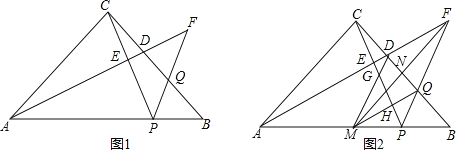
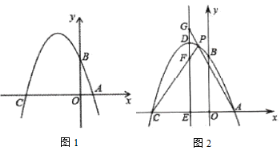
(1)如图1,求证:AF⊥CP;
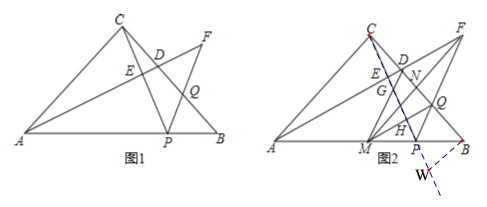
(2)如图2,作∠AFP的平分线FM交AB于点M,交BC于点N,若FN=MN,求证:![]() ;
;
(3)在(2)的条件下,连接DM、MQ,分别交PC于点G、H,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)由∠APC=∠BPQ,得∠ACP=∠PQB,由∠FDQ=∠CDA,∠FQD=∠PQB,推出∠ACP=∠CDA,由∠ACP=∠CDA,推出CP⊥AF;
(2)作WB⊥BC,交CP延长线于点W,由△ACD≌△CBW,QBPWBP,得出CD=QB,由FM平分∠DFQ,DF=FQ,,得到 ND=NQ,FN⊥BC,
由MN=FN=![]() ,得到 DN=
,得到 DN=![]() DC,由DN=NQ,得到DQ=
DC,由DN=NQ,得到DQ=![]() BC;
BC;
(3)易证四边形DFQM是平行四边形,进而得△EDG~△HQP,即可求解.
(1)∵∠APC=∠BPQ,∠A=∠B,∠APC+∠A+∠ACP=∠BPQ+∠B+∠PQB=180°,
∴∠ACP=∠PQB,
∵FD=FQ,
∴∠FQD=∠FDQ,
又∵∠FDQ=∠CDA, ∠FQD=∠PQB,
∴∠CDA=∠PQB,
∴∠ACP=∠CDA,
∴∠CDA +∠BCP =∠ACP+∠BCP=∠ACB=90°,
∴AF⊥CP;
(2)作WB⊥BC,交CP延长线于点W,
∵∠ABC=∠PBW=45°,PB=PB,∠BPF=∠APC=∠BPW,
∴QBPWBP(ASA),
∴BQ=BW,
∵∠BCP+∠ACP=∠ACP+∠CAD=90°,
∴∠BCP=∠CAD,
∵AC=BC,∠ACD=∠CBW=90°,
∴ACDCBW(ASA),
∴CD=BW,
∴BQ= CD,
∵FM平分∠DFQ,DF=FQ,
∴ ND=NQ,FN⊥BC,
∴FN∥AC,
∵CD+DN=BQ+QN,
∴CN=BN,
∴MN是BAC的中位线,
∴MN=FN=![]() ,
,
∴![]() ,即:DN=
,即:DN=![]() ,
,
∴DN=NQ=![]() =
=![]() ,
,
∴DQ= CD=BQ,
∴DQ=![]() BC;
BC;
(3)∵DN=NQ,MN=FN,
∴四边形DFQM是平行四边形,
∴AF∥MQ,DM∥FP,
∴∠EGD=∠HPQ,∠DEG=∠QHP=90°,
∴△EDG~△HQP ,
∴![]() .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】鄂北公司以10元/千克的价格收购一批产品进行销售,为了得到日销售量y(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)请你根据表中的数据确定y与x之间的函数表达式;
(2)鄂北公司应该如何确定这批产品的销售价格,才能使日销售利润W1元最大?
(3)若鄂北公司每销售1千克这种产品需支出a元(a>0)的相关费用,当20≤x≤25时,鄂北公司的日获利W2元的最大值为1215元,求a的值.