[题目]如图.在矩形纸片ABCD中.AB＝8.AD＝17.折叠纸片使点B落在边AD上的E处.折痕为PQ．当E在AD边上移动时.折痕的端点P.Q也随着移动．若限定P.Q分别在边BA.BC上移动.则点E在边AD上移动的最大距离为( )A.6B.7C.8D.9 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在矩形纸片ABCD中，AB＝8，AD＝17，折叠纸片使点B落在边AD上的E处，折痕为PQ．当E在AD边上移动时，折痕的端点P，Q也随着移动．若限定P，Q分别在边BA，BC上移动，则点E在边AD上移动的最大距离为（　　）

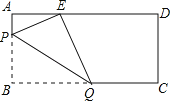
A.6B.7C.8D.9

【答案】A

【解析】

分别利用当点P与点A重合时，以及当点C与点Q重合时，求出AE的极值进而得出答案．

解：如图1，当点P与点A重合时，根据翻折对称性可得AE＝AB＝8，

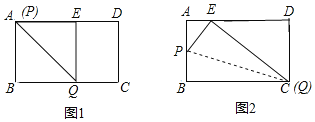
如图2，当点C与点Q重合时，根据翻折对称性可得

QE＝BC＝17，

在Rt△ECD中，EC2＝DE2+CD2，

即172＝（17﹣AE）2+82，

解得：AE＝2，

所以点A'在BC上可移动的最大距离为8﹣2＝6．

故选：A．

练习册系列答案

【题目】如图，在矩形ABCD中，AB＝4，BC＝，E为CD边上一点，将△BCE沿BE折叠，使得C落到矩形内点F的位置，连接AF，若tan∠BAF＝，则CE＝_____．

【题目】如图，已知抛物线y＝ax2+bx+3（a≠0）经过点A(1，0)和点B(3，0)，与y轴交于点C．

（1）求此抛物线的解析式；

（2）若点P是直线BC下方的抛物线上一动点（不点B，C重合），过点P作y轴的平行线交直线BC于点D，设点P的横坐标为m．

①用含m的代数式表示线段PD的长．

②连接PB，PC，求△PBC的面积最大时点P的坐标．

（3）设抛物线的对称轴与BC交于点E，点M是抛物线的对称轴上一点，N为y轴上一点，是否存在这样的点M和点N，使得以点C、E、M、N为顶点的四边形是菱形？如果存在，请直接写出点M的坐标；如果不存在，请说明理由．

【题目】已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系．现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．

水银柱的长度x（cm）	4.2	…	8.2	9.8
体温计的读数y（℃）	35.0	…	40.0	42.0

（1）求y关于x的函数关系式（不需要写出函数的定义域）

（2）用该体温计测体温时，水银柱的长度为6.6cm，求此时体温计的读数．

【题目】如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．

（1）求证：△AEC≌△BED；

（2）若∠1＝50°，则∠BDE＝　　°．

【题目】如图，在三角形ABC中，AB=6，AC=BC=5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E．

（1）求证：DF⊥AC；

（2）求tan∠E的值．

【题目】如图，已知，点绕点顺时针旋转后的对应点落在射线上，点绕点顺时针旋转后的对应点落在射线上，点绕点顺时针旋转后的对应点落在射线上…．连接，依此做法，则=________，=________（用含的代数式表示，为正整数）

【题目】如图，在矩形ABCD中，对角线AC，BD相交于点O，AB＝3cm，BC＝4cm，点E是BC上一点，且CE＝1cm．点P由点C出发，沿CD方向向点D匀速运动，速度为1cm/s；点Q由点A出发，沿AD方向向点D匀速运动，速度为cm/s，点P，Q同时出发，PQ交BD于F，连接PE，QB，设运动时间为t(s)(0＜t＜3)．

(1)当t为何值时，PE∥BD？

(2)设△FQD的面积为y(cm2)，求y与t之间的函数关系式．

(3)是否存在某一时刻t，使得四边形BQPE的周长最小．若存在，求出此四边形BQPE的面积；若不存在，请说明理由．

试题分类