题目内容
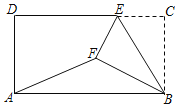
【题目】如图，菱形ABCD中，∠ABC=56°，点E，F分别在BD，AD上，当AE+EF的值最小时，则∠AEF=___度．
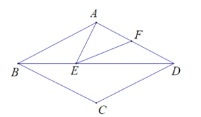
【答案】56
【解析】
连接AC，过点C作CF⊥AD，交BD于点E，交AD于点F，连接AE，根据菱形的性质和垂线段最短可得此时AE＋EF的值最小，且最小值即为CF的长，然后根据等腰三角形的性质、直角三角形的性质和三角形外角的性质即可求出结论．
解：连接AC，过点C作CF⊥AD，交BD于点E，交AD于点F，连接AE
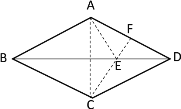
∵四边形ABCD为菱形，∠ABC=56°
∴菱形ABCD是以BD所在直线为对称轴的轴对称图形，∠ADC=∠ABC=56°，DA=DC
∴AE=CE，∠DAC=∠DCA=
（180°－∠ADC）=62°
∴此时AE＋EF=CE＋EF=CF，∠EAC=∠ECA
根据垂线段最短可知：此时AE＋EF的值最小，且最小值即为CF的长
∵CF⊥AD
∴∠AFC=90°
∴∠ECA=90°－∠DAC=28°
∴∠EAC=28°
∴∠AEF=∠EAC＋∠ECA=56°
故答案为：56．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】鄂北公司以10元/千克的价格收购一批产品进行销售，为了得到日销售量y（千克）与销售价格x（元/千克）之间的关系，经过市场调查获得部分数据如表：
销售价格x（元/千克） | 10 | 15 | 20 | 25 | 30 |
日销售量y（千克） | 300 | 225 | 150 | 75 | 0 |
（1）请你根据表中的数据确定y与x之间的函数表达式；
（2）鄂北公司应该如何确定这批产品的销售价格，才能使日销售利润W1元最大？
（3）若鄂北公司每销售1千克这种产品需支出a元（a＞0）的相关费用，当20≤x≤25时，鄂北公司的日获利W2元的最大值为1215元，求a的值．
