题目内容
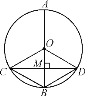
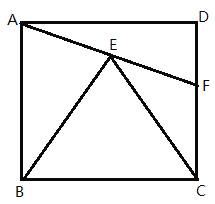
【题目】如图,在正方形![]() 内作正三角形
内作正三角形![]() ,连接
,连接![]() 并延长
并延长![]() 交于F,则
交于F,则![]() 为_______________
为_______________![]() ,若
,若![]() ,则
,则![]() 长度为__________.
长度为__________.
【答案】![]()
![]()
【解析】
由正方形![]() 内作正三角形
内作正三角形![]() ,得∠BAE=∠BEA=75°,从而得∠DAF=15°,即可求出
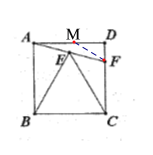
,得∠BAE=∠BEA=75°,从而得∠DAF=15°,即可求出![]() ,在AD边上取点M,使AM=FM,由含30°角的直角三角形的性质,得AM=MF=
,在AD边上取点M,使AM=FM,由含30°角的直角三角形的性质,得AM=MF=![]() ,MD=
,MD=![]() ,进而即可求解.
,进而即可求解.
∵在正方形![]() 内作正三角形
内作正三角形![]() ,
,
∴BE=BC=AB,∠EBC=60°,
∴∠ABE=90°-60°=30°,
∴∠BAE=∠BEA=(180°-30°)÷2=75°,
∴∠DAF=90°-75°=15°,
∴![]() =90°+15°=105°;
=90°+15°=105°;
在AD边上取点M,使AM=FM,则∠MFA=∠MAF=15°,
∴∠DMF=15°+15°=30°,
∵![]() ,
,
∴AM=MF=![]() =
=![]() ,MD=
,MD=![]() ,
,
∴AD=AM+MD=![]() +
+![]() =
=![]() ,
,
∴CD=AD=![]() ,
,
∴![]() =CD-DF=(
=CD-DF=(![]() )-(
)-(![]() )=2.
)=2.
故答案是:105;2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目