题目内容
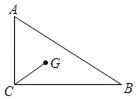
【题目】如图,在△ABC中,∠ABC=90°,AB=6,BC=4,P是△ABC的重心,连结BP,CP,则△BPC的面积为_____.
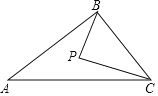
【答案】4
【解析】
△ABC的面积S=![]() AB×BC=
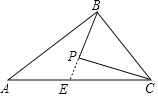
AB×BC=![]() =12,延长BP交AC于点E,则E是AC的中点,且BP=
=12,延长BP交AC于点E,则E是AC的中点,且BP=![]() BE,即可求解.
BE,即可求解.
解:△ABC的面积S=![]() AB×BC=
AB×BC=![]() =12,
=12,
延长BP交AC于点E,则E是AC的中点,且BP=![]() BE,(证明见备注)
BE,(证明见备注)
△BEC的面积=![]() S=6,
S=6,
BP=![]() BE,
BE,
则△BPC的面积=![]() △BEC的面积=4,
△BEC的面积=4,
故答案为:4.
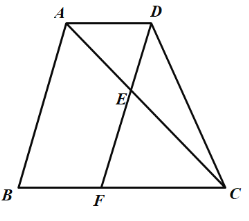
备注:重心到顶点的距离与重心到对边中点的距离之比为2:1,
例:已知:△ABC,E、F是AB,AC的中点.EC、FB交于G.
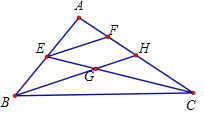
求证:EG=![]() CG 证明:过E作EH∥BF交AC于H.
CG 证明:过E作EH∥BF交AC于H.
∵AE=BE,EH∥BF,
∴AH=HF=![]() AF,
AF,
又∵AF=CF,
∴HF=![]() CF,
CF,
∴HF:CF=![]() ,
,
∵EH∥BF,
∴EG:CG=HF:CF=![]() ,
,
∴EG=![]() CG.
CG.

练习册系列答案
相关题目
【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.