ЬтФПФкШн
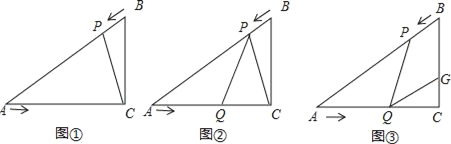
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкRtЁїACBжаЃЌЁЯC=90ЁуЃЌBC=3cmЃЌAC=3![]() cmЃЌЕуPгЩBЕуГіЗЂбиBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛЕуQгЩAЕуГіЗЂбиACЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ
cmЃЌЕуPгЩBЕуГіЗЂбиBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛЕуQгЩAЕуГіЗЂбиACЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() cm/sЃЛШєЩшдЫЖЏЕФЪБМфЮЊt(s)(0ЃМtЃМ3)ЃЌНтД№ЯТСаЮЪЬтЃК
cm/sЃЛШєЩшдЫЖЏЕФЪБМфЮЊt(s)(0ЃМtЃМ3)ЃЌНтД№ЯТСаЮЪЬтЃК
(1)ШчЭМЂйЃЌСЌНгPCЃЌЕБtЮЊКЮжЕЪБЁїAPCЁзЁїACBЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЭМЂкЃЌЕБЕуPЃЌQдЫЖЏЪБЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУЕуPдкЯпЖЮQCЕФДЙжБЦНЗжЯпЩЯЃЌЧыЫЕУїРэгЩЃЛ
(3)ШчЭМЂлЃЌЕБЕуPЃЌQдЫЖЏЪБЃЌЯпЖЮBCЩЯЪЧЗёДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊСтаЮЃПШєДцдкЃЌЪдЧѓГіBGГЄЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)t=![]() ЃЌРэгЩМћНтЮіЃЛ(2)ДцдкЃЌt=1ЃЌРэгЩМћНтЮіЃЛ(3)ВЛДцдкЃЌРэгЩМћНтЮі.
ЃЌРэгЩМћНтЮіЃЛ(2)ДцдкЃЌt=1ЃЌРэгЩМћНтЮіЃЛ(3)ВЛДцдкЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯжБНЧШ§НЧаЮаджЪЃЌгЩЁїAPCЁзЁїACBЃЌЕУ![]() ЃЛЃЈ2ЃЉЙ§ЕуPзїPMЁЭACЃЌИљОнЯпЖЮДЙжБЦНЗжЯпаджЪЃЌЧѓQM,AMЕФБэДяЪНЃЌжЄЁїAPMЁзЁїABCЃЌЕУ
ЃЛЃЈ2ЃЉЙ§ЕуPзїPMЁЭACЃЌИљОнЯпЖЮДЙжБЦНЗжЯпаджЪЃЌЧѓQM,AMЕФБэДяЪНЃЌжЄЁїAPMЁзЁїABCЃЌЕУ ![]() ЃЌ
ЃЌ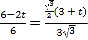 ЃЛЃЈ3ЃЉМйЩшЯпЖЮBCЩЯЪЧДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊЦНааЫФБпаЮЃЌдђPQЁЮBGЃЌPQ=BGЃЌгЩЁїAPQЁзЁїABCЃЌЕУ
ЃЛЃЈ3ЃЉМйЩшЯпЖЮBCЩЯЪЧДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊЦНааЫФБпаЮЃЌдђPQЁЮBGЃЌPQ=BGЃЌгЩЁїAPQЁзЁїABCЃЌЕУ![]() ЃЌ
ЃЌ![]() ЕУBP=2t=3ЃЌЙЪPQЁйBP.
ЕУBP=2t=3ЃЌЙЪPQЁйBP.
(1)дкRtЁїACBжаЃЌЁЯC=90ЁуЃЌAC=3![]() cmЃЌBC=3cmЃЌ
cmЃЌBC=3cmЃЌ
ЁрAB=6ЃЌ
гЩдЫЖЏжЊЃЌBP=2tЃЌAQ= ![]() ЃЌ
ЃЌ
ЁрAP=6Љ2tЃЌ
ЁпЁїAPCЁзЁїACBЃЌ
![]()
Ёрt= ![]() ЃЛ
ЃЛ
(2)ДцдкЃЌ
РэгЩЃКШчЭМЂкЃЌгЩдЫЖЏжЊЃЌBP=2tЃЌAQ=![]() ЃЌ
ЃЌ
ЁрAP=6Љ2tЃЌCQ= ![]() ЃЌ
ЃЌ
ЁпЕуPЪЧCQЕФДЙжБЦНЗжЯпЩЯЃЌ
Й§ЕуPзїPMЁЭACЃЌ
ЁрQM=CM= ![]()

ЁрAM=AQ+QM= ![]() =
=![]() (3+t)
(3+t)
ЁпЁЯACB=90ЁуЃЌЁрPMЁЮBCЃЌ
ЁрЁїAPMЁзЁїABC
Ёр ![]()
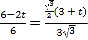
ЁрНтЕУt=1ЃЛ
(3)ВЛДцдк
РэгЩЃКгЩдЫЖЏжЊЃЌBP=2tЃЌ![]() ЃЌ
ЃЌ
ЁрAP=6Љ2tЃЌ
МйЩшЯпЖЮBCЩЯЪЧДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊЦНааЫФБпаЮЃЌ
ЁрPQЁЮBGЃЌPQ=BGЃЌ
ЁрЁїAPQЁзЁїABCЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрBP=2t=3ЃЌ
ЁрPQЁйBPЃЌ
ЁрЦНааЫФБпаЮPQGBВЛПЩФмЪЧСтаЮЃЎМДЃКЯпЖЮBCЩЯВЛДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊСтаЮЃЎ

 КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ
КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИ
ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИ