题目内容
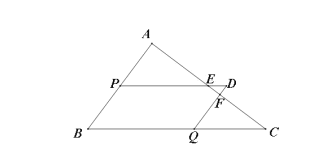
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、点
、点![]() 分别在线段
分别在线段![]() 、线段
、线段![]() 上运动(不包含端点),以
上运动(不包含端点),以![]() 为边作平行四边形
为边作平行四边形![]() ,点
,点![]() 从
从![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位长度,点
个单位长度,点![]() 从
从![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位长度,两点同时出发,当一个点到达终点时,两点都停止运动,运动时间为
个单位长度,两点同时出发,当一个点到达终点时,两点都停止运动,运动时间为![]() 秒.
秒.
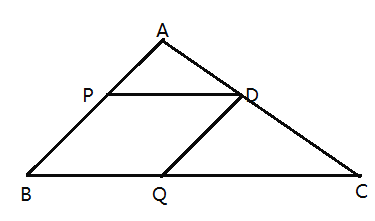
(1)![]() __ ,
__ ,![]() __ _; (用
__ _; (用![]() 表示)
表示)
(2)当平行四边形![]() 为菱形时,求出
为菱形时,求出![]() 值;
值;
(3)![]() 点能否落在线段
点能否落在线段![]() 上?若能,求出
上?若能,求出![]()
(4)当![]() 分别与线段
分别与线段![]() 交于
交于![]() 两点时,求
两点时,求![]() 长度的范围;
长度的范围;
(5)平行四边形![]() 的面积能否为
的面积能否为![]() 面积的一半,若能,请求出
面积的一半,若能,请求出![]() 值,若不能,请说明理由.
值,若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点不能落在线段
点不能落在线段![]() 上,理由详见解析;(4)
上,理由详见解析;(4)![]() ;(5)
;(5)![]() 或
或![]()
【解析】
(1)根据题意,直接写出BP,BQ的值,即可;
(2)根据菱形的性质,得![]() ,进而即可求解;
,进而即可求解;
(3)当![]() 点落在线段
点落在线段![]() 上时,得
上时,得![]() ,得
,得![]() ,结合
,结合![]() ,即可得到结论;
,即可得到结论;
(4)易得![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,根据勾股定理得
,根据勾股定理得![]() ,结合
,结合![]() ,即可得到答案;
,即可得到答案;
(5)过![]() 作
作![]() 于
于![]() ,得
,得![]() ,从而得
,从而得![]() ,结合
,结合![]() ,得
,得![]() ,进而列出方程,即可求解.
,进而列出方程,即可求解.
(1)由题意得:![]() ;
;
(2)当平行四边形![]() 为菱形时,
为菱形时,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴当平行四边形![]() 为菱形时,
为菱形时,![]() ;
;
(3)![]() 点不能落在线段
点不能落在线段![]() 上,理由如下:
上,理由如下:
当![]() 点落在线段
点落在线段![]() 上时,则
上时,则![]() ,
,
![]() ,
,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
即当![]() 点落在线段
点落在线段![]() 上时,
上时,![]() ,
,
这与![]() 矛盾,
矛盾,
![]() 点不能落在线段
点不能落在线段![]() 上;
上;
(4)∵PE∥BC,
∴![]() ,
,
同(3)可得:![]() ,
,
又![]() ,
,
![]() ,
,
∵AP∥FD,
![]() ,
,
![]() ,即:
,即: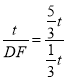 ,
,
∴![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() ,
,
∴![]() ;
;
(5)∵![]() ,
,
∴AC=4,
过![]() 作
作![]() 于
于![]() ,则QG∥AC,
,则QG∥AC,
∴![]() ,
,
![]() ,即:
,即:![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
![]() ,
,
![]()
![]() 或
或![]() .
.


练习册系列答案
相关题目