题目内容
【题目】某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.
(1)求y(元)关于x(元)的函数关系式,并写出x的取值范围.
(2)求当x取何值时y最大?并求出y的最大值.
(3)若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?
【答案】(1)y=﹣10x2+200x+3000(0≤x≤30);(2)当x=10时,y最大=4000;(3)应将该商品降价15元.
【解析】
根据题意构建函数模型求解利润问题.依题意商品降价(x元)与每天销售该商品获得的利润为(y元)存在函数关系:y=(110-80-x)(100+![]() ×50),依据这个二次函数关系式,求出利润的最大值即可.
×50),依据这个二次函数关系式,求出利润的最大值即可.
(1)由题意得:y=(110﹣80﹣x)(100+![]() ×50)
×50)
=﹣10x2+200x+3000 (0≤x≤30)
(2)∵y=﹣10x2+200x+3000
=﹣10(x﹣10)2+4000
∴当x=10时,y最大=4000
(3)当y=3750时,=10x2+200x+3000=3750,解得:x1=5,x2=15.
∵要尽可能最大的向顾客让利,x应该取15;
∴应将该商品降价15元.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】有这样一个问题:探究函数![]()
![]() 的图象与性质,小东根据学习函数的经验,对函数的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
的图象与性质,小东根据学习函数的经验,对函数的图象与性质进行了探究,下面是小东的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值,则
的几组对应值,则![]() .
.
| … |
|
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
|
|
| … |
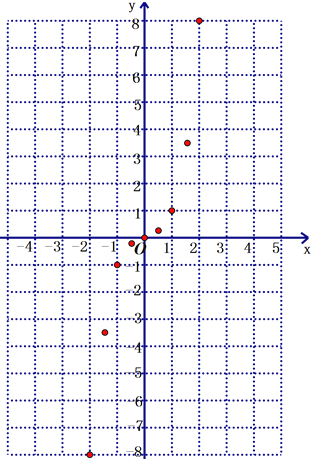
(2)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象;
(3)当![]() 时,
时,![]() 随
随![]() 的增大而 ;当
的增大而 ;当![]() 时,
时,![]() 的最小值为 .
的最小值为 .