题目内容
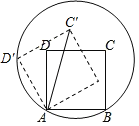
【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不一定成立的是( )
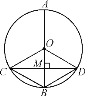
A.CM＝DMB.
C.△OCM≌△ODMD.OM＝MB
【答案】D
【解析】
由直径AB垂直于弦CD，利用垂径定理得到M为CD的中点，B为劣弧
的中点，可得出A和B选项成立，再由OM为公共边，OC=OD，CM=DM，利用SSS可得出三角形OCM与三角形DOM全等，可得出选项C成立，而OM不一定等于MD，得出选项D不成立．
∵AB是⊙O的直径，弦CD⊥AB，垂足为M，
∴M为CD的中点，即CM=DM，选项A成立；
B为
的中点,即
，选项B成立；
在△OCM和△ODM中，
∵
，
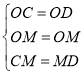∴△OCM和△ODM (SSS)，选项C成立；
而OM与MD不一定相等，选项D不成立.
故选：D.
练习册系列答案
相关题目
