题目内容
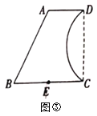
【题目】如图,在平面直角坐标系中,已知点A(8,1),B(0,3),反比例函数![]() (x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(x>0)的图象经过点A,动直线x=t(0<t<8)与反比例函数的图象交于点M,与直线AB交于点N.
(1)求k的值;
(2)求△BMN面积的最大值;
(3)若MA⊥AB,求t的值.
【答案】(1)k=8;(2)△BMN面积最大值为![]() ;(3)
;(3)![]() .
.
【解析】
(1)把点A坐标代入y=![]() (x>0),即可求出k的值;
(x>0),即可求出k的值;
(2)先求出直线AB的解析式,设M(t,![]() ),N(t,
),N(t,![]() t3),则MN=
t3),则MN=![]()
![]() t+3,由三角形的面积公式得出△BMN的面积是t的二次函数,即可得出面积的最大值;
t+3,由三角形的面积公式得出△BMN的面积是t的二次函数,即可得出面积的最大值;
(3)求出直线AM的解析式,由反比例函数解析式和直线AM的解析式组成方程组,解方程组求出M的坐标,即可得出结果.
(1)把点A(8,1)代入反比例函数y=![]() (x>0)得:1=
(x>0)得:1=![]() ,
,
∴k=8;
(2)设直线AB的解析式为:y=kx+b(k≠0),
根据题意得:![]() ,
,
解得:k=![]() ,b=3,
,b=3,
∴直线AB的解析式为:y=![]() x3,
x3,
设M(t,![]() ),则N(t,
),则N(t,![]() t3),
t3),
∴MN=![]()
![]() t+3,
t+3,
∴△BMN的面积S=![]() (
(![]()
![]() t+3)·t=
t+3)·t=![]() t2+
t2+![]() t+4=
t+4=![]() (t3)2+
(t3)2+![]() ,
,
∵![]() <0,
<0,
∴S有最大值,
当t=3时,△BMN的面积的最大值为![]() ;
;
(3)∵MA⊥AB,
∴设直线MA的解析式为:y=2x+c,
把点A(8,1)代入得:1=2×8+c,解得:c=17,
∴直线AM的解析式为:y=2x+17,
联立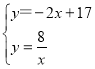 ,解得:
,解得: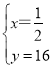 或
或![]() (舍去),
(舍去),
∴M的坐标为(![]() ,16),
,16),
∴t=![]() .
.

练习册系列答案
相关题目