题目内容
【题目】如图,大楼![]() (可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点
(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点![]() 和点
和点![]() 处,
处,![]() 、
、![]() 均在
均在![]() 的中垂线上,且
的中垂线上,且![]() 、
、![]() 到大楼的距离分别为
到大楼的距离分别为![]() 米和
米和![]() 米,又已知
米,又已知![]() 长
长![]() 米,
米,![]() 长
长![]() 米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.
米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.

【答案】![]()
【解析】
据已知首先得出DH=HP=x米,NO=(20![]() +40-x)米,PO=(60+x)米,再利用平行线分线段成比例定理和三角形面积求出即可.
+40-x)米,PO=(60+x)米,再利用平行线分线段成比例定理和三角形面积求出即可.
连接MD并延长,连接NC并延长,使其两延长线相交于点P,
作PO⊥MN于O,作CG⊥MP于G,
根据题意可得出:
ME=60,DE=HO=FC=60米,FN=20![]() 米,EF=40,
米,EF=40,
∴NC=![]() ,
,
=40![]() 米,
米,
设EO=x米,
∴DH=x米,
∵ME=DE=60米,
∴∠MDE=45,
∴DH=HP=x米,NO=(20![]() +40x)米,PO=(60+x)米,
+40x)米,PO=(60+x)米,
∵FC∥PO,
∴![]() ,
,
∴x![]() ,
,
解得:x=6020![]() ,
,
∴PO=(12020![]() )米,NO=(40
)米,NO=(40![]() 20)米,
20)米,
![]() CDHP=
CDHP=![]() DPCG,
DPCG,
![]() ×40×(12020
×40×(12020![]() 60)=
60)= ![]() ×
×![]() [20
[20![]() +40(40
+40(40![]() 20)]CG,
20)]CG,
CG=20![]() 米,
米,
∴行走的最短距离长为:NC+CG=(40![]() +20
+20![]() )米.
)米.
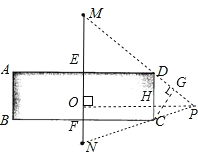
故答案为:40![]() +20
+20![]()

练习册系列答案
相关题目