题目内容
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=![]() PQ.
PQ.

【答案】(1)AC4+2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)利用角平分线定理求出FM,再利用等腰直角三角形的性质即可得出CF,最后用![]() 即可;
即可;
(2)先判断出![]() ,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
(1)如图1,
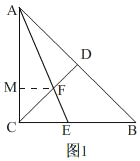
∵等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
∴CD⊥AB,∠ACD=45°
过点F作FM⊥AC,
∵AE平分∠CAB,
∴FM=FD=2
在Rt△CMF中,∠ACD=45°,
∴![]()
∴![]()
∵CD是等腰直角三角形斜边的中线,
∴![]()
(2)如图2,连接DP,DQ,

∵△ADC绕点D顺时针旋转一定角度得到△ADN,
∴AN=BC,DN=CD=DB,△ADN是等腰直角三角形,
∵△BCD是等腰直角三角形,点Q是BC中点,
∴![]()
∵点P是AN中点,
∴![]()
∴![]()
∵∠NDP=∠CDQ=45°,
∴∠PDQ=∠PDN+∠CDN+∠CDQ=90°+∠CDN,
∵∠NDB=∠CDN+∠CDB=90°+∠CDN,
∴∠PDQ=∠NDB,
∵![]()
∴△PDQ∽△NDB,
∴![]()
∴![]()

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目