ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮAOBCжаЃЌACЁЮOBЃЌЖЅЕуOЪЧдЕуЃЌЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌACЃН24cmЃЌOBЃН26cmЃЌЕуPДгЕуAГіЗЂЃЌвд1cm/sЕФЫйЖШЯђЕуCдЫЖЏЃЌЕуQДгЕуBЭЌЪБГіЗЂЃЌвд3m/sЕФЫйЖШЯђЕуOдЫЖЏЃЎЙцЖЈЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЛДгдЫЖЏПЊЪМЃЌЩшPЃЈQЃЉЕудЫЖЏЕФЪБМфЮЊtsЃЎ
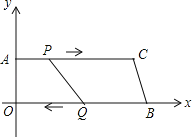
ЃЈ1ЃЉЧѓжБЯпBCЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЫФБпаЮAOQPЪЧОиаЮЃП
ЁОД№АИЁП(1) yЃНЉ4x+104ЃЛ (2) ЕБtЮЊ6.5sЪБЃЌЫФБпаЮAOQPЪЧОиаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШИљОнЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌAC=24cmЃЌOB=26cmЃЌЗжБ№ЧѓГіЕуBЁЂCЕФзјБъИїЪЧЖрЩйЃЛШЛКѓгІгУД§ЖЈЯЕЪ§ЗЈЃЌЧѓГіжБЯпBCЕФКЏЪ§НтЮіЪНМДПЩЃЎ
ЃЈ2ЃЉИљОнЫФБпаЮAOQPЪЧОиаЮЃЌПЩЕУAP=OQЃЌОнДЫЧѓГіtЕФжЕЪЧЖрЩйМДПЩЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌ
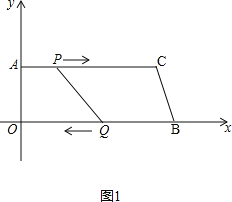
ЁпЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ8ЃЉЃЌACЃН24 cmЃЌOBЃН26 cmЃЌ
ЁрBЃЈ26ЃЌ0ЃЉЃЌCЃЈ24ЃЌ8ЃЉЃЌ
ЩшжБЯпBCЕФКЏЪ§НтЮіЪНЪЧyЃНkx+bЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФКЏЪ§НтЮіЪНЪЧyЃНЉ4x+104ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌ
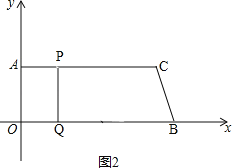
ИљОнЬтвтЕУЃКAPЃНt cmЃЌBQЃН3t cmЃЌдђOQЃНOBЉBQЃНЃЈ26Љ3tЃЉcmЃЌ
ЁпЫФБпаЮAOQPЪЧОиаЮЃЌ
ЁрAPЃНOQЃЌ
ЁрtЃН26Љ3tЃЌ
НтЕУtЃН6.5ЃЌ
ЁрЕБtЮЊ6.5sЪБЃЌЫФБпаЮAOQPЪЧОиаЮЃЎ







