题目内容
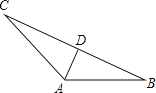
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且![]() +(a+2b-4)2=0.
+(a+2b-4)2=0.
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM=![]() S△ABC,求出点M的坐标.
S△ABC,求出点M的坐标.
(3)在坐标轴的其他位置是否有在点M,使S△COM=![]() S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.
S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.

【答案】(1)a=2,b=3;(2)(0,5);(3)(0,-5)或(-2.5,0)或(2.5,0).
【解析】
(1)根据非负数的性质列出关于a、b的二元一次方程组,求解即可;
(2)根据三角形的面积公式列式求出OM的长,然后写出点M的坐标即可;
(3)写出点M在y轴负半轴上时的坐标,再求出点M在x轴上,根据三角形的面积公式列式求出OM的长,然后写出点M的坐标.
解:(1)由题意得,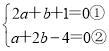 ,
,
①×2得,4a+2b+2=0③,
③②得,3a=6,
解得a=2,
把a=2代入①得,4+b+1=0,
解得b=3;
(2)∵a=2,b=3,C(1,2),
∴AB=3(2)=5,点C到y轴的距离为1,
∴![]() OM1=
OM1=![]() ×
×![]() ×5×2,
×5×2,
解得OM=5,
∵点M在y轴正半轴上,
∴M的坐标为(0,5);
(3)存在.
点M在y轴负半轴上时,点M(0,-5),
点M在x轴上时,![]() OM2=
OM2=![]() ×
×![]() ×5×2,
×5×2,
解得OM=2.5,
所以,点M的坐标为(-2.5,0)或(2.5,0),
综上所述,存在点M的坐标为(0,-5)或(-2.5,0)或(2.5,0).

练习册系列答案
相关题目