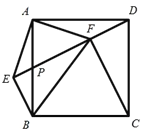
题目内容
【题目】在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 、
、![]() 均在线段
均在线段![]() 上,且
上,且![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .在
.在![]() 中,若
中,若![]() 轴,
轴,![]() 轴,则称
轴,则称![]() 为点
为点![]() 、
、![]() 的“榕树三角形”.
的“榕树三角形”.
(1)若点![]() 坐标为
坐标为![]() ,且
,且![]() ,则点
,则点![]() 、
、![]() 的“榕树三角形”的面积为 .
的“榕树三角形”的面积为 .
(2)当点![]() 、
、![]() 的“榕树三角形”是等腰三角形时,求点
的“榕树三角形”是等腰三角形时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,作过![]() 、
、![]() 、
、![]() 三点的抛物线
三点的抛物线![]() .
.
①若![]() 点必为抛物线上一点,求点
点必为抛物线上一点,求点![]() 、
、![]() 的“榕树三角形”面积
的“榕树三角形”面积![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
②当点![]() 、
、![]() 的“榕树三角形”面积2,且抛物线
的“榕树三角形”面积2,且抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点时,直接写出
的“榕树三角形”恰有两个交点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)点B的坐标为
;(2)点B的坐标为![]() ;(3)①
;(3)①![]() ;②m=-2或-4≤m≤-3
;②m=-2或-4≤m≤-3
【解析】
(1)待定系数法求直线AB解析式,根据“榕树三角形”新定义和三角形面积即可求出结论;
(2)依据等腰直角三角形性质即可求得点B的坐标;
(3)①先利用待定系数法求得线段AB的表达式,再根据“榕树三角形”新定义求出点M的坐标,再利用三角形面积即可求得S与m之间的函数关系式;
②抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点时,可分两种情况:点P在对称轴右侧或点P在对称轴左侧(包括对称轴上),分别进行讨论即可.
的“榕树三角形”恰有两个交点时,可分两种情况:点P在对称轴右侧或点P在对称轴左侧(包括对称轴上),分别进行讨论即可.
解:(1)设直线AB解析式为:y=kx+b,则
![]() ,解得
,解得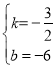
∴直线AB解析式为:![]() ,
,
当x=-1时,![]() ,
,
∴P(-1,![]() ),
),
∵PM∥x轴,BM∥y轴,
∴M(-4, ![]() ),
),
∴PM=3,BM=![]() ,
,
∴![]() .
.
(2)根据题意得,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴点B的坐标为![]() .
.
(3)①首先,确定自变量取值范围为![]() ,
,
由(2)易得,线段![]() 的表达式为
的表达式为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
由于抛物线![]() 经过
经过![]() 、
、![]() 两点,
两点,
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]()
![]() ,
,
![]() ,
,
故![]() ,
,
②∵点P、Q的“榕树三角形”面积为2,
∴![]() ,
,
∴PM=2,
∴M(m-2,-m-6),
∵抛物线![]() 与点
与点![]() 、
、![]() 的“榕树三角形”恰有两个交点,
的“榕树三角形”恰有两个交点,
∴可分两种情况:点P在对称轴右侧或点P在对称轴左侧(包括对称轴上),
若点P在对称轴右侧时,m>-3,此时两个交点关于直线x=-3对称,
∴![]() ,
,
解得:m=-2或m=-4,
∵m>-3,
∴m=-2,
若点P在对称轴左侧(包括对称轴上),即m≤-3,
此时两个交点分别在PM、QM边上,
∴m-2≥-6,即m≥-4,
∴-4≤m≤-3,
综上所述,m的取值范围为m=-2或-4≤m≤-3.

 计算高手系列答案
计算高手系列答案