Question

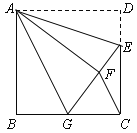
【题目】在正方形 ABCD 中， P 为 AB 的中点，的延长线于点 E ，连接 AE 、 BE ， 交 DP 于点 F ，连接 BF 、FC ，下列结论：① ；② FB AB ；③ ；④ FC EF . 其中正确的是（ ）

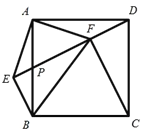
A.①②④B.①③④C.①②③D.①②③④

Answer 1

【答案】D

【解析】

根据已知和正方形的性质推出∠EAB=∠DAF，∠EBA=∠ADP，AB=AD，证△ABE≌△ADF即可；取EF的中点M，连接AM，推出AM=MF=EM=DF，证∠AMB=∠FMB，BM=BM，AM=MF，推出△ABM≌△FBM即可；求出∠FDC=∠EBF，推出△BEF≌△DFC即可．

解：∵正方形ABCD，BE⊥ED，EA⊥FA，
∴AB=AD=CD=BC，∠BAD=∠EAF=90°=∠BEF，
∵∠APD=∠EPB，
∴∠EAB=∠DAF，∠EBA=∠ADP，
∵AB=AD，
∴△ABE≌△ADF，∴①正确；
∴AE=AF，BE=DF，
∴∠AEF=∠AFE=45°，
取EF的中点M，连接AM，
∴AM⊥EF，AM=EM=FM，
∴BE∥AM，
∵AP=BP，
∴AM=BE=DF，
∴∠EMB=∠EBM=45°，
∴∠AMB=90°+45°=135°=∠FMB，
∵BM=BM，AM=MF，
∴△ABM≌△FBM，
∴AB=BF，∴②正确；
∴∠BAM=∠BFM，
∵∠BEF=90°，AM⊥EF，
∴∠BAM+∠APM=90°，∠EBF+∠EFB=90°，
∴∠APF=∠EBF，
∵AB∥CD，
∴∠APD=∠FDC，
∴∠EBF=∠FDC，
∵BE=DF，BF=CD，
∴△BEF≌△DFC，
∴CF=EF，∠DFC=∠FEB=90°，
∴③正确；④正确；

故选D．