题目内容
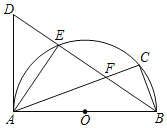
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.
(1)求证:AD为⊙O切线;
(2)若AB=20,tan∠EBA=![]() ,求BC的长.
,求BC的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先利用角平分线定义、圆周角定理证明∠4=∠2,再利用AB为直径得到∠2+∠BAE=90°,则∠4+∠BAE=90°,然后根据切线的判定方法得到AD为⊙O切线;
(2)解:根据圆周角定理得到∠ACB=90°,设AE=3k,BE=4k,则AB=5k=20,求得AE=12,BE=16,连接OE交AC于点G,如图,解直角三角形即可得到结论.
(1)证明:∵BE平分∠ABC,
∴∠1=∠2,
∵AB为直径,
∴AE⊥BD,
∵DE=FE,
∴∠3=∠4,
∵∠1=∠3,
∴∠4=∠2,
∵AB为直径,
∴∠AEB=90°,
∵∠2+∠BAE=90°
∴∠4+∠BAE=90°,即∠BAD=90°,
∴AD⊥AB,
∴AD为⊙O切线;
(2)解:∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,∵tan∠EBA=![]() ,
,
∴设AE=3k,BE=4k,则AB=5k=20,
∴AE=12,BE=16,
连接OE交AC于点G,如图,
∵∠1=∠2,
∴![]() ,
,
∴OE⊥AC,
∵∠3=∠2,
∴tan∠EBA=tan∠3=![]() ,
,
∴设AG=4x,EG=3x,
∴AE=5x=12,
∴x=![]() ,
,
∴AG=![]() ,
,
∵OG∥BC,
∴AC=2AG=![]() ,
,
∴BC=![]() =
=![]() .
.


练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目