题目内容
【题目】在平面直角坐标系xOy中,抛物线y=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,AB=4,点D为抛物线的顶点.
(1)求点A和顶点D的坐标;
(2)将点D向左平移4个单位长度,得到点E,求直线BE的表达式;
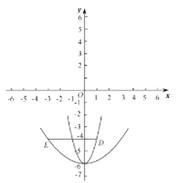
(3)若抛物线y=ax2﹣6与线段DE恰有一个公共点,结合函数图象,求a的取值范围.
【答案】(1)A(﹣1,0),顶点D(1,﹣4);(2)直线BE的表达式为![]() ;(3)
;(3)![]() .
.
【解析】
(1)令y=0,则mx2+(m3)x3=0,可求得x1=1,![]() ,即可求得A(1,0),由AB=4,即可求得B(3,0),得到m=1,则解析式为y=x22x3,化成顶点式即可求得顶点坐标;
,即可求得A(1,0),由AB=4,即可求得B(3,0),得到m=1,则解析式为y=x22x3,化成顶点式即可求得顶点坐标;
(2)根据平移的性质得到E点的坐标,然后根据待定系数法即可求得;
(3)把点D(1,4),E(3,4)分别代入y=ax26,求得a的值,即可求得.
解:(1)y=mx2+(m﹣3)x﹣3与y轴交于点C(0,﹣3),
令y=0,则mx2+(m﹣3)x﹣3=0,
可得x1=﹣1,![]() ,
,
由于点A在点B左侧,m>0可知点A(﹣1,0),
又∵AB=4,
∴点B(3,0),
∴m=1,
∴y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴点D(1,﹣4);
(2)依题意可知点E(﹣3,﹣4),
设直线BE的表达式为y=kx+b,
∴![]() ,
,
解得,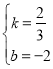
∴直线BE的表达式为![]() ;
;
(3)点D(1,﹣4),E(﹣3,﹣4)分别代入y=ax2﹣6,
可得![]() 或a=2,
或a=2,
∴a的取值范围为![]() .
.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目