题目内容
如图,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从A点、C点同时出发,均以2cm/s的速度分别沿AD向D点和沿CB向B点运动。

(1)经过几秒首次可使EF⊥AC?
(2)若EF⊥AC,在线段AC上,是否存在一点P,使 ?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。

(1)经过几秒首次可使EF⊥AC?
(2)若EF⊥AC,在线段AC上,是否存在一点P,使
 ?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。解:(1)设经过x秒首次可使EF⊥AC,AC与EF相交于点O,

则AE=2x,CF=2x。
∵四边形ABCD是矩形,∴∠EAO=∠FCO,∠AOE=∠COF。
∴△AOE≌△COF(AAS)。∴AO=OC,OE=OF。
∵AB=12cm,AD=16cm,
∴根据勾股定理得AC=20cm。∴OC=10cm。
在Rt△OFC中, ,∴
,∴ 。
。
过点E作EF⊥BC交BC于点H,
在Rt△EFN中, ,∴
,∴ 。
。
解得 。
。
∴经过 秒首次可使EF⊥AC。
秒首次可使EF⊥AC。
(2)过点E作EP⊥AD交AC于点P,则P就是所求的点。证明如下:
由作法,∠AEP=900,
又EF⊥AC,即∠AOE=900。∴△AEP∽△AOE。
∴ ,即
,即 。
。
∴ 。
。

则AE=2x,CF=2x。
∵四边形ABCD是矩形,∴∠EAO=∠FCO,∠AOE=∠COF。
∴△AOE≌△COF(AAS)。∴AO=OC,OE=OF。
∵AB=12cm,AD=16cm,
∴根据勾股定理得AC=20cm。∴OC=10cm。
在Rt△OFC中,
 ,∴
,∴ 。
。 过点E作EF⊥BC交BC于点H,
在Rt△EFN中,
 ,∴
,∴ 。
。解得
 。
。∴经过
 秒首次可使EF⊥AC。
秒首次可使EF⊥AC。(2)过点E作EP⊥AD交AC于点P,则P就是所求的点。证明如下:
由作法,∠AEP=900,
又EF⊥AC,即∠AOE=900。∴△AEP∽△AOE。
∴
 ,即
,即 。
。∴
 。
。(1)设经过x秒首次可使EF⊥AC,AC与EF相交于点O,过点E作EF⊥BC交BC于点H,由AAS证明△AOE≌△COF,得到AO=OC,OE=OF,从而求得OC=10cm,在Rt△OFC中,由勾股定理得 。因此,在Rt△EFN中, 由勾股定理得
。因此,在Rt△EFN中, 由勾股定理得 ,即
,即 ,解出即可。
,解出即可。
(2)证明△AEP∽△AOE即可得出结论。
 。因此,在Rt△EFN中, 由勾股定理得
。因此,在Rt△EFN中, 由勾股定理得 ,即
,即 ,解出即可。
,解出即可。(2)证明△AEP∽△AOE即可得出结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,求
,求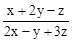 的值.
的值.
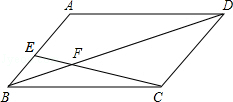


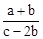 的值是
的值是 ,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.