题目内容
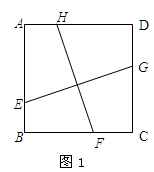
如图1,点C将线段AB分成两部分,如果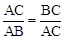 ,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.

(1)如图2,在△ABC中,∠A=360°,AB=AC,∠C的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
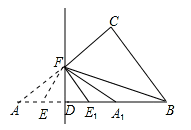
(2)若△ABC在(1)的条件下,如图(3),请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
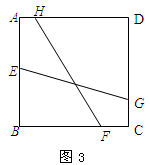
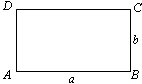
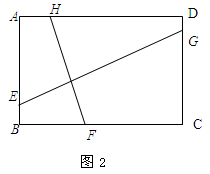
(3)如图4,在直角梯形ABCD中,∠D=∠C=900,对角线AC、BD交于点F,延长AB、DC交于点E,连接EF交梯形上、下底于G、H两点,请问直线GH是不是直角梯形ABCD的黄金分割线,并证明你的结论.
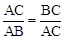 ,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果
,那么称点C为线段AB的黄金分割点。某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.
(1)如图2,在△ABC中,∠A=360°,AB=AC,∠C的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图(3),请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图4,在直角梯形ABCD中,∠D=∠C=900,对角线AC、BD交于点F,延长AB、DC交于点E,连接EF交梯形上、下底于G、H两点,请问直线GH是不是直角梯形ABCD的黄金分割线,并证明你的结论.
(1)点D是AB边上的黄金分割点(2)直线CD是△ABC的黄金分割线(3)GH不是直角梯形ABCD的黄金分割线
解:(1)点D是AB边上的黄金分割点,证明如下:
∵∠A=360°,AB=AC,∴∠B=∠ACB=720。
∵CD平分∠ACB,∴∠DCB=360。∴∠BDC=∠B=720。
∵∠A=∠BCD,∠B=∠B,∴△BCD∽△BAC。∴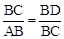 。
。
又∵BC=CD=AD,∴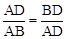 。
。
∴点D是AB边上的黄金分割点。
(2)直线CD是△ABC的黄金分割线,证明如下:
设△ABC的边AB上的高为h,则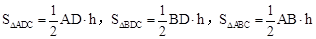 ,
,
∴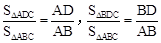 。
。
∵D是AB的黄金分割点,∴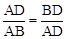 。∴
。∴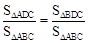 。
。
∴直线CD是△ABC的黄金分割线。
(3)GH不是直角梯形ABCD的黄金分割线,证明如下:
∵BC∥AD,∴△EBG∽△EAH,△EGC∽△EHD。∴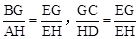 。
。
∴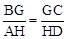 ,即
,即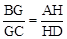 。
。
同理,由△BGF∽△DHF,△CGF∽△AHF得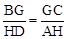 ,即
,即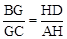 。
。
∴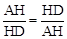 。∴AH=HD。∴BG=GC。
。∴AH=HD。∴BG=GC。
∴梯形ABGH与梯形GHDH上下底分别相等,高也相等。
∴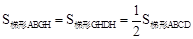 。
。
∴GH不是直角梯形ABCD的黄金分割线。
(1)由等腰三角形角和边的关系,根据△BCD∽△BAC得到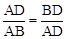 而证明。
而证明。
(2)根据黄金分割线的定义证明直线CD是△ABC的黄金分割线。
(3)反复应用相似三角形的相似比得出梯形ABGH与梯形GHDH上下底分别相等,高也相等的结论,从而得到GH不是直角梯形ABCD的黄金分割线的结论。
∵∠A=360°,AB=AC,∴∠B=∠ACB=720。
∵CD平分∠ACB,∴∠DCB=360。∴∠BDC=∠B=720。
∵∠A=∠BCD,∠B=∠B,∴△BCD∽△BAC。∴
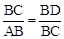 。
。又∵BC=CD=AD,∴
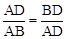 。
。∴点D是AB边上的黄金分割点。
(2)直线CD是△ABC的黄金分割线,证明如下:
设△ABC的边AB上的高为h,则
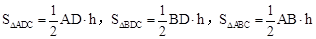 ,
,∴
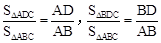 。
。∵D是AB的黄金分割点,∴
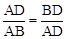 。∴
。∴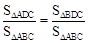 。
。∴直线CD是△ABC的黄金分割线。
(3)GH不是直角梯形ABCD的黄金分割线,证明如下:
∵BC∥AD,∴△EBG∽△EAH,△EGC∽△EHD。∴
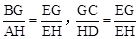 。
。∴
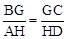 ,即
,即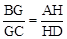 。
。同理,由△BGF∽△DHF,△CGF∽△AHF得
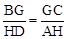 ,即
,即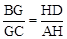 。
。∴
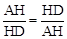 。∴AH=HD。∴BG=GC。
。∴AH=HD。∴BG=GC。∴梯形ABGH与梯形GHDH上下底分别相等,高也相等。
∴
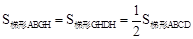 。
。∴GH不是直角梯形ABCD的黄金分割线。
(1)由等腰三角形角和边的关系,根据△BCD∽△BAC得到
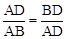 而证明。
而证明。(2)根据黄金分割线的定义证明直线CD是△ABC的黄金分割线。
(3)反复应用相似三角形的相似比得出梯形ABGH与梯形GHDH上下底分别相等,高也相等的结论,从而得到GH不是直角梯形ABCD的黄金分割线的结论。

练习册系列答案
相关题目
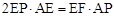 ?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
 ︰1,猜想BF︰FC= ;并证明你的结论
︰1,猜想BF︰FC= ;并证明你的结论 

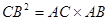
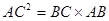
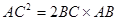
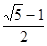 AB
AB
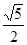 (如图3),试求EG的长度。
(如图3),试求EG的长度。