题目内容
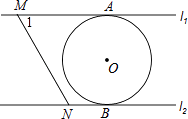
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,若tan∠ABO= ![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m). 
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
【答案】
(1)解:∵在直角△BCE中,tan∠ABO= ![]() =
= ![]() ,BE=OE+OB=4+2=6,
,BE=OE+OB=4+2=6,
∴EC=BEtan∠ABO=6× ![]() =3.
=3.
∴C的坐标是(﹣2,3).
设反比例函数的解析式是y= ![]() .
.
把C的坐标代入得:3= ![]() ,
,
解得:k=﹣6,
则反比例函数的解析式是:y=﹣ ![]()
B的坐标是(4,0).
∵在直角△AOB中,tan∠ABO= ![]() =
= ![]() ,
,
∴OA=OBtan∠ABO=4× ![]() =2,
=2,
则A的坐标是(0,2),
设直线AB的解析式是y=kx+b,
根据题意得: ![]() ,
,
解得: 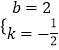 .
.
则直线AB的解析式是:y=﹣ ![]() x+2
x+2
(2)解:解方程组: 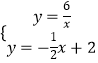 ,
,
解得: ![]() 或
或 ![]() ,
,
则D的坐标是:(6,﹣1).
∵OA=2
∴S△COD=S△OAC+S△OAD= ![]() ×2×2+
×2×2+ ![]() ×2×6=2+6=8
×2×6=2+6=8
【解析】(1)在直角△BCE中,BE=6,利用三角函数即可求得CE的长,则C的坐标即可求解,然后利用待定系数法即可求得反比例函数的解析式;(2)在直角△ABO中,利用三角函数即可求得OA的长,则A,B的坐标已知,利用待定系数法即可求得直线的解析式;(3)首先求得D的坐标,根据S△COD=S△OAC+S△OAD即可求解.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).

【题目】按下列程序计算,把答案填写在表格内,然后观察有什么规律,想一想:为什么会有这个规律?
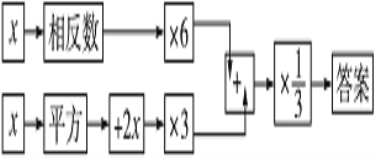
(1)填写表内空格:
输入 | -3 | -2 | -1 | 0 | … |
输出答案 | 9 |
|
|
| … |
(2)发现的规律是:输入数据x,则输出的答案是__________;
(3)为什么会有这个规律?请你说明理由.