题目内容
【题目】已知：抛物线y=ax2﹣2（a﹣1）x+a﹣2（a＞0）．
（1）求证：抛物线与x轴有两个交点；
（2）设抛物线与x轴有两个交点的横坐标分别为x1 ， x2 ， （其中x1＞x2）．若y是关于a的函数，且y=ax2+x1 ， 求这个函数的表达式；
（3）在（2）的条件下，结合函数的图象回答：若使y≤﹣3a2+1，则自变量a的取值范围为 ． 
【答案】
（1）证明：∵△=4（a﹣1）2﹣4a（a﹣2）=4＞0，
∴抛物线与x轴有两个交点
（2）解：解方程得x= 
，
∴x=1或x=1﹣ 
，
∵a＞0，x1＞x2，
∴x1=1，x2=1﹣ ，
∴y=a（1﹣ ）+1=a﹣1（a＞0）
（3）0＜a≤ 
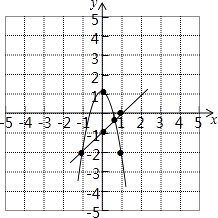
【解析】（3）解：画出直线y=a﹣1和抛物线y=﹣3a2+1的图象，如图，
解方程得到a﹣1=﹣3a2+1得a=﹣1或a= ，
即直线y=a﹣1和抛物线y=﹣3a2+1的图象的交点坐标为（﹣1，﹣2）、（ ，﹣ 
），
当﹣1≤a≤ 时，a﹣1≤﹣3a2+1，
而a＞0，
∴a的取值范围为0＜a≤ ．
所以答案是0＜a≤ ．
【考点精析】利用抛物线与坐标轴的交点对题目进行判断即可得到答案，需要熟知一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
阅读快车系列答案
【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的限距点的定义如下：若P′为直线PC与⊙C的一个交点，满足r≤PP′≤2r，则称P′为点P关于⊙C的限距点，如图为点P及其关于⊙C的限距点P′的示意图． 
（1）当⊙O的半径为1时．
①分别判断点M（3，4），N（ 
，0），T（1， 
）关于⊙O的限距点是否存在？若存在，求其坐标；
②点D的坐标为（2，0），DE，DF分别切⊙O于点E，点F，点P在△DEF的边上．若点P关于⊙O的限距点P′存在，求点P′的横坐标的取值范围；
（2）保持（1）中D，E，F三点不变，点P在△DEF的边上沿E→F→D→E的方向运动，⊙C的圆心C的坐标为（1，0），半径为r，请从下面两个问题中任选一个作答．
问题1 | 问题2 |
若点P关于⊙C的限距点P′存在，且P′随点P的运动所形成的路径长为πr，则r的最小值为 | 若点P关于⊙C的限距点P′不存在，则r的取值范围为 |
