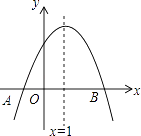题目内容
【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 . 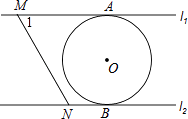
【答案】![]() 或
或 ![]()
【解析】解: 当MN在左侧与⊙O相切时,连接OM、OA,如图1,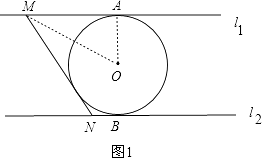
∵MA、MN是⊙O的切线,
∴OM平分∠AMN,OA⊥MA,
∴∠AMO=30°,
∴OM=2OA=2,
在Rt△OAM中,MA= ![]() =
= ![]() ;
;
当MN在右侧与⊙O相切时,连接OM、OA,如图2,
∵∠1=60°,
∴∠AMN=120°,
同上可知∠AMO= ![]() ∠AMN=60°,
∠AMN=60°,
∴OM=2AM,
在Rt△OAM中,MA2=OM2﹣OA2 , 即MA2=4MA2﹣1,解得MA= ![]() ;
;
综上可知MA的长度为 ![]() 或
或 ![]() ,
,
所以答案是: ![]() 或
或 ![]() .
.
【考点精析】关于本题考查的平行线的性质和切线的性质定理,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是( )
A.抛物线的开口向下
B.当x>﹣3时,y随x的增大而增大
C.二次函数的最小值是﹣2
D.抛物线的对称轴是x=﹣ ![]()