题目内容
【题目】折叠矩形纸片:
第一步,如图1,在纸片一端折出一个正方形MBCN,再把纸片展开;
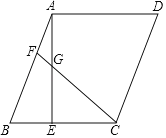
第二步,如图2,把这个正方形对折,再把纸片展开,得矩形MAEN和ABCE;
第三步,如图3,折出矩形ABCE的对角线EB,并把EB折到图中所示的ED处;
第四步,如图4,展平纸片,按所得点D折出DF,得矩形BFDC.
(1)若MN=2时,CM=________;
(2)![]() 的值为 ________.
的值为 ________.

【答案】![]()
![]()
【解析】
(1)由等腰直角三角形的性质和勾股定理,即可求出CM的长度;
(2)设正方形的边长为2a,由折叠的性质,可得EC=正方形的边长×![]() ,在Rt△ABC中,利用勾股定理可求出AB与正方形的边长之间的关系,再求出CD=
,在Rt△ABC中,利用勾股定理可求出AB与正方形的边长之间的关系,再求出CD=![]() ,即可求解.
,即可求解.
解:(1)∵四边形MBCN是正方形,MC是对角线,
∴MN=CN=2,
由勾股定理,得:![]() ;
;
故答案为:![]() ;
;
(2)在正方形BCNM中,设NC=2a=BC,
∵E为NC的中点,
∴EC=![]() .
.
在Rt△EBC中,EB=![]() .
.
又∵ED=EB,
∴CD=ED![]() EC=(
EC=(![]() )a.
)a.
∴![]() ;
;
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目