Question

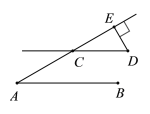
【题目】(1)如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A＝30°，求∠D的度数．

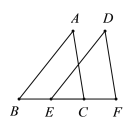
（2）如图，E，C在BF上，AB＝DE，AC＝DF，BE＝CF,试说明：AC∥DF.

Answer 1

【答案】（1）53°；（2）证明见解析

【解析】

(1)运用平行线性质，及三角形内角和定理可求得；（2）证△ABC≌△DEF

得∠ACB＝∠F，故AC∥DF.

（1）解： ∵AB∥CD

∴∠ECD＝∠A＝37°（两直线平行，同位角相等）

∵在△CDE中，DE⊥AE

∴∠CED＝90°

∴∠D＝180°－∠ECD－∠CED＝180°－90°－37°＝53°

(2）∵BE＝CF，

∴BC＝EF

在△ABC和△DEF中

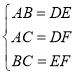
∴△ABC≌△DEF

∴∠ACB＝∠F

∴AC∥DF