题目内容
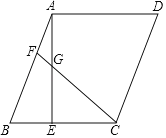
【题目】在ABCD中,AE⊥BC于点E,F为AB边上一点,连接CF,交AE于点G,CF=CB=AE.
(1)若AB![]() ,BC
,BC![]() ,求CE的长;
,求CE的长;
(2)求证:BE=CG﹣AG.
【答案】(1)![]() 1;(2)见解析.
1;(2)见解析.
【解析】
(1)在Rt△ABE中,由勾股定理求得BE,再由线段和差求得结果;
(2)延长GA到H,使得AH=BE,证明△ADH≌△EAB得DH=AB=CD,得∠DCH=∠DHC,再证明∠GHC=∠GCH得GC=GH便可得结果.
(1)∵CF=CB=AE,BC![]() ,
,
∴AE![]() ,
,
∵AE⊥BC于点E,AB![]() ,
,
∴BE![]() ,
,
∴CE=BC﹣BE![]() 1;
1;
(2)延长GA到H,使得AH=BE,连接DH,CH,
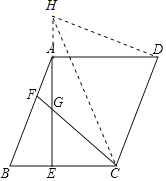
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵AE⊥BC,
∴∠AEB=∠DAE=90°,
∵BC=AE,
∴AE=DA,
在△ADH和△EAB中,
 ,
,
∴△ADH≌△EAB(SAS),
∴DH=DC,∠DHA=∠ABE,
∴∠DHC=∠DCH,
∵CB=CF,
∴∠CBF=∠CFB,
∵AB∥CD,
∴∠CFB=∠DCF,
∴∠CBF=∠DCF,
∵∠DHA=∠ABE,
∴∠DHA=∠DCF,
∵∠DHC=∠DCH,
∴∠CHG=∠HCG,
∴CG=HG,即CG=AG+AH,
∴AH=CG﹣AG,
∵AH=BE,
∴BE=CG﹣AG,

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目