题目内容
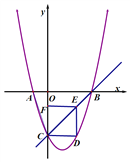
【题目】如图,在直角坐标系中,直线y=x-3交x轴于点B,交y轴于点C,抛物线经过点A(-1,0),B,C三点,点F在y轴负半轴上,OF=OA.
(1)求抛物线的解析式;
(2)在第一象限的抛物线上存在一点P,满足S△ABC=S△PBC,请求出点P的坐标;
(3)点D是直线BC的下方的抛物线上的一个动点,过D点作DE∥y轴,交直线BC于点E,①当四边形CDEF为平行四边形时,求D点的坐标;
②是否存在点D,使CE与DF互相垂直平分?若存在,请求出点D的坐标;若不存在,请说明理由.


【答案】(1) y=(x+1)(x-3)=x2-2x-3;
(2) P(4,5)
(3)①D(1,-4)或(2,-3),
②存在D(2,-3),使CE与DF互相垂直平分,理由见解析.
【解析】试题分析:(1)先根据直线解析式确定出B 、C的坐标,然后利用待定系数法即可得;
(2)过点A作AP∥BC,交抛物线于P点,P点满足S△ABC=S△PBC,求出AP的解析式,然后与抛物线的解析式联立组成方程组,求解即可得;
(3)根据点E在BC上,点D在抛物线上,设D(x,x2-2x-3),E(x,x-3),则DE= -x2+3x,
①四边形CDEF为平行四边形可知DE=CF=2,解方程即可得;
②当四边形CDEF为正方形时,才有CE与DF互相垂直平分,据此即可得.
试题解析:(1)由直线y=x-3与坐标轴交于B、C两点,则有B(3,0),C(0,-3),
由题意设抛物线得解析式为y=a(x+1)(x-3),
将C点坐标代入,得-3=-3a,
解得,a=1,
∴抛物线解析式为y=(x+1)(x-3)=x2-2x-3;
(2)过点A作AP∥BC,交抛物线于P点,P点满足S△ABC=S△PBC,
设直线AP的解析式为y=x+b,则0=-1+b,∴b=1,
∴直线AP的解析式为y=x+1,
由![]() 解得,
解得, ![]()
∴P(4,5);
(3)易得F(0,-1),CF=2,
设D(x,x2-2x-3),E(x,x-3),则DE=x-3-(x2-2x-3)=-x2+3x,
①令-x2+3x=2,解得x3=1,x4=2,
D(1,-4)或(2,-3),
②存在,
当D(2,-3)时E(2,-1),EF⊥CF,且EF=CF,
∴平行四边形CDEF为正方形,
∴CE与DF互相垂直平分。
∴存在D(2,-3),使CE与DF互相垂直平分.

【题目】某学习小组做了一个实验:从一幢100 m高的楼顶随手放下一只苹果,测得有关数据如下:
下落时间t(s) | 1 | 2 | 3 | 4 |
下落高度h(m) | 5 | 20 | 45 | 80 |
则下列说法错误的是( )
A. 苹果每秒下落的路程越来越长 B. 苹果每秒下落的路程不变
C. 苹果下落的速度越来越快 D. 可以推测,苹果落到地面的时间不超过5秒