题目内容
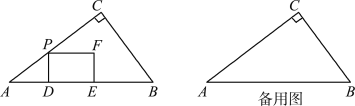
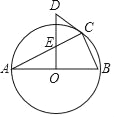
【题目】如图,![]() 是半圆的直径,
是半圆的直径,![]() 为半圆
为半圆![]() 的圆心,
的圆心,![]() 是弦,取
是弦,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
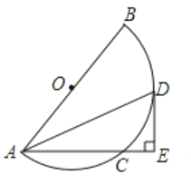
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,直接写出
时,直接写出![]() 面积最大时,点
面积最大时,点![]() 到直径
到直径![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接OD,先说明∠BAD=∠CAD,然后根据等腰三角形的性质和平行线的性质证得OD//AC,再运用平行线的性质∠ODE=90°即可;
(2)连接BC、OC,则∠ACB是直角,利用特殊锐角三角函数值可得∠BAC=30°,则∠BOC=60°,最后依据扇形的弧长公式进行计算即可;
(3)连接OD、BC、OC,过点O作OF⊥AC,垂足为F,先证明四边形ODEF为矩形,得到OF=ED,再通过解直角三角形求得AC、OF,最后运用角平分线定理即可解答.
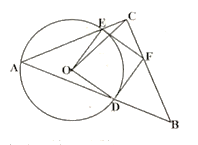
解:(1)证明:如解图①,连接![]()
![]() 是的中点,
是的中点,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]()
又![]() 是半圆
是半圆![]() 的半径,
的半径,
![]() 是半圆
是半圆![]() 的切线;
的切线;
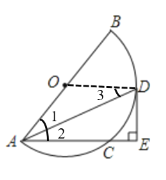
图①
(2)如解图②,连接![]() 、
、![]() ,则
,则![]() 是直角.
是直角.
∵![]() ,
,![]() ,
,
∴![]()
![]() ,
,![]()
![]()
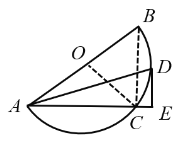
图②
(3)如解图③所示:连接![]() 、
、![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
∵![]() .
.
![]()
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,
当![]() 时,
时,![]() 为等腰直角三角形,此时
为等腰直角三角形,此时![]() 面积最大,
面积最大,
![]() ·
·![]()
![]()
![]() ,
,
![]() 平分
平分![]()
![]() 点
点![]() 到
到![]() 的距离
的距离![]() .
.
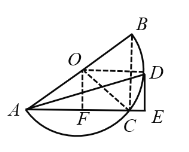
图③

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目